VECTORES

Representación gráfica de un vector fijo

Un vector fijo $\overrightarrow{AB}$ es un segmento orientado que va del punto $A$ (origen) al punto $B$ (extremo).

Elementos de un vector

1 Dirección de un vector: La dirección del vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

2 Sentido de un vector: El sentido del vector $\overrightarrow{AB}$ es el que va desde el origen $A$ al extremo $B$ .

3 Módulo de un vector:

Representación gráfica del módulo de un vector

El módulo del vector $\overrightarrow{AB}$ es la longitud del segmento $AB$ , se representa por $\left | \overrightarrow{AB} \right |$ .

El módulo de un vector es un número siempre positivo o cero.

Módulo de un vector a partir de sus componentes

$\vec{u}=(u_{1},u_{2})$

$\left | \vec{u} \right |=\sqrt{u_{1}^{2}+u_{2}^{2}}$

Ejemplo

$\vec{u}=(3,4)$ $\left | \vec{u} \right |=\sqrt{3^{2}+4^{2}}=\sqrt{25}=5$

Módulo a partir de las coordenadas de los puntos:

$A(x_{1},y_{1})$ $B(x_{2},y_{2})$

$\left | \overrightarrow{AB} \right |=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$

Ejemplo

$A(2,1)$ $B(-3,2)$ $\left | \overrightarrow{AB} \right |=\sqrt{(-3-2)^{2}+(2-1)^{2}}=\sqrt{26}$

4 Coordenadas de un vector

Representación gráfica de las coordenadas de un vector

Si las coordenadas de los puntos extremos, $A\; \textup{y}\; B$ , son:

$A(x_{1},y_{1})$ $A(x_{2},y_{2})$

Las coordenadas del vector $\overrightarrow{AB}$ son las coordenadas del extremo menos las coordenadas del origen.

$\overrightarrow{AB}=(x_{2}-x_{1},y_{2}-y_{1})$

Ejemplo:

$A(2,2)$ $B(5,7)$

$\overrightarrow{AB}=(5-2,7-2)$ $\overrightarrow{AB}=(3,5)$

Clases de vectores

1 Vectores equipolentes

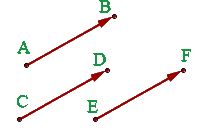
Ejemplo de vectores equipolentes representación gráfica

Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.

2 Vectores libres

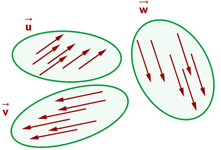
Ejemplos de vectores libres representación gráfica

El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Cada vector fijo es un representante del vector libre.

3 Vectores fijos:

Ejemplo de vector fijo representación gráfica

Un vector fijo es un representante del vector libre. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y origen.

4 Vectores ligados

Ejemplo de vectores ligados representación gráfica

Los vectores ligados son vectores equipolentes que actúan en la misma recta. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y se encuentran en la misma recta.

5 Vectores opuestos

Ejemplo de vectores opuestos representación gráfica

Los vectores opuestos tienen el mismo módulo, dirección, y distinto sentido.

$\vec{u}=(u_{1},u_{2})$

$-\vec{u}=(-u_{1},-u_{2})$

6 Vectores unitarios

Ejemplo de un vector unitario representación gráfica

Los vectores unitarios tienen de módulo, la unidad.

Para obtener un vector unitario, de la misma dirección y sentido que el vector dado se divide éste por su módulo.

$\vec{u}=\cfrac{\vec{v}}{\left | \vec{v} \right |}$

7 Vectores concurrentes

Ejemplo de vectores concurrentes representación gráfica

Los vectores concurrentes tienen el mismo origen.

8 Vectores de posición

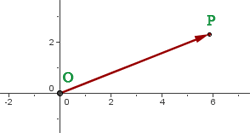
Ejemplo de vector de posición representación gráfica

El vector $\overrightarrow{OP}$ que une el origen de coordenadas $O$ con un punto $P$ se llama vector de posición del punto $P$ .

9 Vectores linealmente dependientes:

Ejemplo de vectores linealmente dependientes representación gráfica

Varios vectores libres del plano son linealmente dependientes si existe una combinación lineal de ellos que sea igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.

$a_{1}\vec{v_{1}}+a_{2}\vec{v_{2}}+...+a_{n}\vec{v_{n}}=0$

10 Vectores linealmente independientes

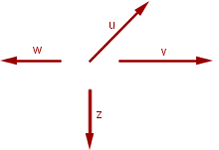
Ejemplo de vectores linealmente independientes representación gráfica

Varios vectores libres son linealmente independientes si ninguno de ellos se puede expresar como combinación lineal de los otros.

$a_{1}\vec{v_{1}}+a_{2}\vec{v_{2}}+...+a_{n}\vec{v_{n}}=0$

$a_{1}=a_{2}=...=a_{n}=0$

11 Vectores ortogonales

Ejemplo de vectores ortogonales representación gráfica

Dos vectores son ortogonales o perpendiculares si su producto escalar es cero.

$\vec{u}\cdot \vec{v}=0$ $u_{1}\cdot v_{1}+u_{2}\cdot v_{2}=0$

12 Vectores ortonormales

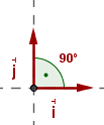
Ejemplo de vectores ortonormales representación gráfica

Dos vectores son ortonormales si:

a Su producto escalar es cero.

b Los dos vectores son unitarios.

Una vez que ya conocemos la definición de un vector, procederemos a estudiar algunas de las operaciones básicas que se pueden realizar entre vectores.

Suma de vectores

Si tenemos dos vectores $\vec{u} = (u_1, u_2)$ y $\vec{v} = (v_1, v_2)$ , entonces la suma de $\vec{u}$ y $\vec{v}$ es

$\displaystyle \vec{u} + \vec{v} = (u_1 + v_1, u_2 + v_2)$

En otras palabras, el vector suma de $\vec{u}$ y $\vec{v}$ es el vector que resulta de sumar las componentes respectivas de estos vectores: la primera componente de $\vec{u}$ se suma con la primera componente de $\vec{v}$ , y la segunda componente de $\vec{u}$ se suma con la segunda componente de $\vec{v}$ .

Interpretación gráfica de la suma

Observemos la siguiente gráfica que muestra la suma de los vectores $\vec{u}$ y $\vec{v}$ :

representación gráfica de la suma de dos vectores u y v

Si $\vec{u}$ y $\vec{v}$ son dos vectores libres, entonces para sumarlos gráficamente primero se elige el representante de $\vec{v}$ cuyo origen es el extremo de $\vec{u}$ . Luego, $\vec{u} + \vec{v}$ es el vector cuyo origen es el origen de $\vec{u}$ y cuyo extremo es el extremo de $\vec{v}$ .

Notemos que también se puede elegir un representante de $\vec{u}$ tal que su origen sea el extremo de $\vec{v}$ . La suma $\vec{u} + \vec{v}$ tendrá el mismo valor, pero ahora la obtendremos uniendo el origen de $\vec{v}$ con el extremo de $\vec{u}$ .

Regla del paralelogramo

Lo que discutimos anteriormente como la suma gráfica de los vectores se conoce como regla del paralelogramo. En particular, si queremos sumar dos vectores libres con origen en común, entonces debemos trazar rectas paralelas a los vectores. De esta forma se obtiene un paralelogramo cuya diagonal —que inicia en el origen de los vectores— es la suma misma de los vectores.

Observa la siguiente figura que muestra la regla del paralelogramo.

regla del paralelogramo representacion grafica con los vectores u y v

Resta de vectores

La resta de dos vectores $\vec{u}$ y $\vec{v}$ simplemente es la suma de $\vec{u}$ con $-\vec{v}$ (es decir, el opuesto de $\vec{v}$ ).

De este modo, si consideramos los componentes de $\vec{u}$ y $\vec{v}$ , entonces la resta está dada por

$\displaystyle \vec{u} - \vec{v} = \vec{u} + \left(- \vec{v}\right) = (u_1 - v_1, u_2 - v_2)$

Gráficamente, la resta de $\vec{u}$ y $\vec{v}$ se obtiene igual que la suma. La única diferencia es que sumamos el opuesto de $\vec{v}$ . Observa la siguiente figura que muestra a $\vec{u} - \vec{v}$ y nota que en el extremo de $\vec{u}$ se coloca el origen de $- \vec{v}$ .

resta de u y v representacion grafica vectores

Observemos que la resta $\vec{u} - \vec{v}$ gráficamente es el vector que une el extremo de $\vec{v}$ con el extremo de $\vec{u}$ tal y como se puede apreciar en la siguiente figura:

Producto de vector por escalar

La multiplicación de un vector $\vec{u}$ por un número $k$ se escribe $k\vec{u}$ o $k \cdot \vec{u}$ . El número $k$ también se conoce como escalar. Además, la multiplicación por escalar es otro vector que satisface las siguientes propiedades:

$k\vec{u}$ tiene la misma dirección que $\vec{u}$ .
Si $k$ es positivo, entonces $k\vec{u}$ tiene el mismo sentido que $\vec{u}$ .
Si $k$ es negativo, entonces $k\vec{u}$ tiene el sentido contrario que $\vec{u}$ .
El módulo de $k\vec{u}$ es $| k | \cdot \left|\vec{u} \right|$

Observemos la siguiente figura que representa la multiplicación de $\vec{u}$ por 3.

multiplicacion de un vector u por 3 representacion grafica

En términos de componentes, si $\vec{u} = (u_1, u_2)$ , entonces la multiplicación por escalar está dada por

$\displaystyle k\vec{u} = (k \cdot u_1, k \cdot u_2)$

Ejemplos de ejercicios con vectores

Consideremos los vectores $\vec{u} = (-2, 5)$ y $\vec{v} = (3, -1)$ . Entonces:

1 La suma está dada por:

$\displaystyle \vec{u} + \vec{v} = (-2 +3 , 5 - 1) = (1, 4)$

2 La resta es:

$\displaystyle \vec{u} - \vec{v} = \left(-2 - 3 , 5 - (-1) \right) = (-5, 6)$

3 El opuesto de $\vec{u}$ es:

$\displaystyle -\vec{u}= \left( 2 , -5 \right)$

4 El producto escalar de $\vec{v}$ por 3 está dado por:

$\displaystyle 3 \vec{v}= \left( 9 , -3 \right)$

Definición y propiedades

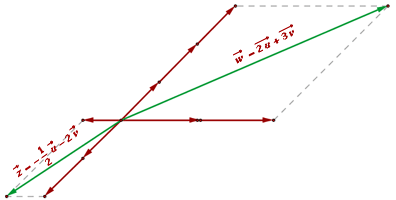
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por algunos escalares. Es decir, una combinación lineal es una expresión de la forma:

$\displaystyle \vec{v} = a_1 \vec{v_1} + a_2 \vec{v_2} + \cdots + a_n \vec{v_n}$

Para el caso particular de dos vectores $\vec{u}$ , $\vec{v}$ , y dos números $a,b$ , entonces una combinación lineal de $\vec{u}$ y $\vec{v}$ está dada por el vector $a\vec{u}+b\vec{v}$ .

La siguiente figura muestra la representación gráfica del vector $\displaystyle \vec{w} = 2\vect{u} + 3\vect{v}$ .

combinacion lineal de los vectores u y v

Nota: Cualquier vector en el plano se puede poner como combinación lineal de otros dos vectores que tengan distinta dirección. Asimismo, esta combinación lineal es única.

Ejemplos

1Dados los vectores $\vec{x} = (1, 2)$ y $\vec{y} = (3, -1)$ , hallar el vector combinación lineal $\vec{z} = 2\vec{x} + 3\vec{y}$ .

Solución: Para encontrar el vector $\vec{z}$ , simplemente realizamos las operaciones necesarias:

$\displaystyle \vec{z} = 2(1, 2) + 3(3, -1) = (2, 4) + (9, -3) = (11, 1)$

Por lo que,

$\displaystyle \vec{z} = (11, 1)$

2 Expresa al vector $\vec{z} = (2, 1)$ como una combinación lineal de los vectores $\vec{x} = (3, -2)$ y $\vec{y} = (1, 4)$ .

Solución: Supongamos que $\vec{z}$ se puede escribir como una combinación lineal de $\vec{x}$ y $vec{y}$ , es decir, existen constantes $a, b$ tales que $\vec{z} = a \vec{x} + b\vec{y}$ . Por lo tanto, solo debemos encontrar estas constantes:

$(2, 1) = a(3, -2) + b(1, 4) = (3a, -2a) + (b, 4b)$

Por tanto, tenemos que

$(2, 1) = (3a + b, -2a + 4b)$

Es decir, las constantes $a, b$ deben resolver el siguiente sistema de ecuaciones lineal:

$\displaystyle \begin{cases} 3a + b = 2\\ -2a + 4b = 1 \end{cases}$

Cuya solución está dada por

$\displaystyle a = \frac{1}{2}, \quad b = \frac{1}{2}$

De este modo, $\vec{z}$ se puede escribir como

$\displaystyle \vec{z} = \frac{1}{2} \vec{x} + \frac{1}{2} \vec{y}$

Vectores linealmente dependientes

Un conjunto de vectores se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal. Es decir,

$a_1 \vec{v}_1+a_2 \vec{v}_2+...+a_n \vec{v}_n=\vec{0}$ y $a_i\not =0$ para algún valor de $i=1,2,...,n$

Propiedades

1 Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.

$a_1 \vec{v}_1+a_2 \vec{v}_2+...+a_n \vec{v}_n=\vec{0}$

Si $\displaystyle a_1 \not =0$ entonces $\displaystyle \vec{v}_1=-\frac{a_2}{a_1}\vec{v}_2-\frac{a_3}{a_1}\vec{v}_3-...-\frac{a_n}{a_1}\vec{v}_n$

También se cumple el recíproco: si un vector es combinación lineal de otros, entonces todos los vectores son linealmente dependientes.

2 Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.
3 Dos vectores del plano $\vec{u}=(u_1,u_2)$ y $\vec{v}=(v_1,v_2)$ son linealmente dependientes si sus componentes son proporcionales.

$\vec{u}=k\vec{v} \hspace{1cm} \Rightarrow \hspace{1cm} (u_1,u_2)=k(v_1,v_2)$

$\displaystyle \frac{u_1}{v_1}=\frac{u_2}{v_2}=k$

Vectores linealmente independientes

Un conjunto de vectores se dice linealmente independiente si ninguno de ellos puede ser escrito con una combinación lineal de los restantes. Por lo que la siguiente expresión

$a_1 \vec{v}_1+a_2 \vec{v}_2+...+a_n \vec{v}_n=\vec{0}$

Será cierta sólo cuando todos los coeficientes sean iguales a cero.

$a_1=a_2 =...=a_n=0$

Los vectores linealmente independientes en el plano tienen distinta dirección y sus componentes no son proporcionales.

Ejemplo:

Determinar si son linealmente dependientes o independientes los vectores.

$\vec{u}=(3,1)$
$\vec{v}=(2,3)$

$\displaystyle \frac{3}{2}\not =\frac{1}{3} \hspace{1cm}\text{pues}\hspace{1cm} 3\cdot 3 \not=2\cdot 1$

Como sus componentes no son proporcionales entonces, son linealmente independientes.

¿Como se forma la base de dos vectores?

Dos vectores $\vec{u}$ y $\vec{v}$ con distinta dirección forman una base, porque cualquier vector del plano se puede poner como combinación lineal de ellos.

$\vec{x}=a\vec{u}+b\vec{v}$

Las coordenadas del vector respecto a la base son:

$\vec{x}=(a,b)$

Ejemplo:

$\displaystyle \begin{matrix} \vec{w}=2\vec{u}+3\vec{v}\; \; & & \vec{w}=(2,3) \\ & & \\ \vec{z}=-\cfrac{1}{2}\vec{u}-2\vec{v} & & \; \; \; \; \; \; \; \vec{z}=\left ( -\cfrac{1}{2},-2 \right ) \end{matrix}$

Los dos vectores que forman una base no pueden ser paralelos.

Clasificación de bases

Base ortogonal

Los dos vectores de la base son perpendiculares entre sí.

Base ortonormal

Vectores ortonormales representación gráfica

Los dos vectores de la base son perpendiculares entre sí, y además tienen módulo $1$ .

$\left \{ \vec{i},\vec{j} \right \}$

$\begin{matrix} \vec{i}=(1,0) & & \vec{i}=(0,1)\\ & & \\ \vec{i}\perp \vec{j}\; \; \; \; \; \; & & \; \; \; \; \left | \vec{i} \right |=\left | \vec{j} \right |=1 \end{matrix}$

Esta base formada por los vectores $\vec{i}$ y $\vec{j}$ se denomina base canónica.

Es la base que se utiliza habitualmente, de modo que si no se advierte nada se supone que se está trabajando en esa base.

Ejemplos:

1¿Qué pares de los siguientes vectores forman una base?

$\vec{u}=(2,-3) \ \ \ \ \ \ \ \ \ \ \vec{v}=(5,1) \ \ \ \ \ \ \ \ \ \ \vec{w}=(-4,6)$

Sabemos que si los vectores son paralelos, no pueden formar una base. Entonces, para averiguar cuales de los vectores anteriores la forman, vamos a tomarlos por pares y comprobar si son paralelos o no.

Primero, estudiamos los vectores $\vec u$ y $\vec v$ :

$\displaystyle \cfrac{2}{-3}=\cfrac{5}{1} \ \ \ \ \ \ \ \ \ \ 2\neq 15$

Los vectores $\vec u$ y $\vec v$ no son paralelos, y entonces forman una base: $\left \{ \vec{u}, \vec{v} \right \}$

Seguimos comparando los vectores $\vec u$ y $\vec w$ :

$\displaystyle \cfrac{2}{-3}=\cfrac{-4}{6} \ \ \ \ \ \ \ \ \ \ 12=12$

Los vectores $\vec u$ y $\vec w$ son los dos iguales a $12$ , entonces paralelos. No forman una base.

Por ultimo, estudiamos los vectores $\vec v$ y $\vec w$ :

$\displaystyle \cfrac{5}{1}=\cfrac{-4}{6} \ \ \ \ \ \ \ \ \ \ 30\neq 4$

Los vectores $\vec v$ y $\vec w$ no son paralelos, y entonces forman una base: $\left \{ \vec{v}, \vec{w} \right \}$

2Sean los vectores libres $\vec{u}=(2,1)$ , $\vec{v}=(1,4)$ y $\vec{w}=(5,6)$ . Determinar:

A Si forman una base $\vec{u}$ y $\vec{w}$ .

Para comprobar si forman una base, seguimos los mismos pasos que en el ejemplo anterior para ver si son paralelos o no:

$\displaystyle \cfrac{2}{1}=\cfrac{1}{4} \ \ \ \ \ \ \ \ \ \ 2\cdot 4\neq 1\cdot 1$

Los dos vectores no son paralelos, entonces forman una base:

$\left \{ \vec{u}, \vec{w} \right \}$

B Expresar $\vec{w}$ como combinación lineal de los de la base

Sabemos que:

$\vec{x}=a\vec{u}+b\vec{v}$

Entonces:

$(5,6)=a(2,1)+b(1,4)$

$\left\{\begin{matrix} 5=2a+b\\ 6=a+4b \end{matrix}\right. \; \; \; \; \; \Rightarrow \; \; \; \; \; a=2\; \; \; \; \; b=1$

La combinación lineal es:

$\vec{w}=2\vec{u}+\vec{v}$

3 Un vector $\vec{w}$ tiene de coordenadas $(3, 5)$ en la base canónica.

¿Qué coordenadas tendrá referido a la base $\vec{u}=(1,2)$ , $\vec{v}=(2,1)$ ?

$(3,5)=a(1,2)+b(2,1)$

$5=2a+b$

$3 = a + 2b$

Rasolvemos el sistema de ecuaciones:

Sabiendo que:

$3 = a + 2b$

Despejamos la incógnita $a$ :

$a=3-2b$

Sustituimos el valor de $a$ en la segunda ecuación:

$5=2a+b$

$5=2(3-2b)+b$

$5=6-4b+b$

$5=6-3b$

$3b=6-5$

$3b=1$

$\displaystyle b=\frac{1}{3}$

Teniendo el valor de $b$ , lo sustituimos en la primera ecuación:

$a=3-2b$

$\displaystyle a=3-2(\frac{1}{3})$

$\displaystyle a= 3 - \frac{2}{3}$

$\displaystyle a= \frac{9}{3} - \frac{2}{3}$

$\displaystyle a= \frac{7}{3}$

Las coordenadas de $\displaystyle \vec{w}$ en la base $B$ son $\left ( \cfrac{7}{3},\cfrac{1}{3} \right )$ .

En el plano, un sistema de referencia está constituido por un punto O del plano y una base ( , ).

El punto O del sistema de referencia se llama origen.

Los vectores , no paralelos forman la base.

1

Ortogonal

Los vectores base son perpendiculares y tienen distinto módulo.

2

Ortonormal

Los vectores de la base son perpendiculares y unitarios, es decir, de módulo 1.

Se representan por las letras .

Las rectas OX, OY se llaman ejes de coordenadas o ejes coordenados cartesianos.

Coordenadas del punto medio de un segmento

Las coordenadas del punto medio de un segmento son la semisuma de las coordenadas de los extremos.

Ejemplo:

Hallar las coordenadas del punto medio del segmento AB.

Condición para que tres puntos estén alineados

Los puntos A (x₁, y₁), B(x₂, y₂) y C(x₃, y₃) están alineados siempre que los vectores tengan la misma dirección. Esto ocurre cuando sus coordenadas son proporcionales.

Ejemplo:

Calcular el valor de a para que los puntos estén alineados.

Simétrico de un punto respecto de otro

Si A’ es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA’. Por lo que se verificará igualdad:

Ejemplo:

Hallar el simétrico del punto A(7, 4) respecto de M(3, – 11).

Coordenadas del baricentro

Baricentro o centro de gravedad de un triángulo es el punto de intersección de sus medianas.

Las coordenadas del baricentro son:

Ejemplo:

Dados los vértices de un triángulo A(-3, -2), B(7, 1) y C(2, 7), hallar las coordenadas del baricentro.

División de un segmento en una relación dada

Dividir un segmento AB en una relación dada r es determinar un punto P de la recta que contiene al segmento AB, de modo que las dos partes, PA y PB, están en la relación r:

Ejemplo:

¿Qué puntos P y Q dividen al segmento de extremos A(-1, -3) y B(5, 6) en tres partes iguales?

El producto escalar de dos vectores es una operación que toma dos vectores y produce un número real:

$\displaystyle k = \vec{u} \cdot \vec{v}$

Observemos que el producto escalar se suele denotar por medio de un punto $\vec{u} \cdot \vec{v}$ . Otra notación que se suele utilizar es $\displaystyle \langle \vec{u}, \vec{v} \rangle$ . Sin embargo, en Superprof siempre denotaremos el producto escalar utilizando un punto.

Además, el producto escalar no debe confundirse con la multiplicación de un vector por un escalar.

Maneras de calcular el producto escalar

Existen dos maneras equivalentes de obtener el producto escalar de dos vectores $\vec{u}$ y $\vec{v}$ . Estas se describen a continuación:

1 Si conocemos el módulo de de ambos vectores y el ángulo $\alpha$ que forman entre ellos, entonces el producto escalar se obtiene mediante

$\displaystyle \vec{u} \cdot \vec{v} = \left| \vec{u} \right| \left| \vec{v} \right| \cos \alpha$

2 Si conocemos los componentes de los vectores $\vec{u} = (u_1, u_2)$ y $\vec{v} = (v_1, v_2)$ , entonces el producto escalar está dado por

$\displaystyle \vec{u} \cdot \vec{v} = u_1v_1 + u_2v_2$

Ejemplos

1 Consideremos los vectores $\vec{u} = (3, 0)$ y $\vec{v} = (5, 5)$ . Asimismo, el ángulo entre los vectores es $\alpha = 45^{\circ}$ .

Para calcular el producto escalar, primero debemos encontrar el módulo de $\vec{u}$ y $\vec{v}$ :

$\displaystyle \left| \vec{u} \right| = \sqrt{3^2 + 0^2} = 3, \qquad \left| \vec{v} \right| = \sqrt{5^2 + 5^2} = \sqrt{50} = 5\sqrt{2}$

De este modo, el producto escalar está dado por

$\displaystyle \vec{u} \cdot \vec{v} = 3 \cdot 5\sqrt{2} \cdot \cos\left( 45^{\circ} \right) = 15\sqrt{2} \cdot \frac{\sqrt{2}}{2} = 15$

2 Repetiremos el ejemplo anterior con $\vec{u} = (3, 0)$ y $\vec{v} = (5, 5)$ . Sin embargo, ahora utilizaremos la otra fórmula:

$\displaystyle \vec{u} \cdot \vec{v} = 3 \cdot 5 + 0 \cdot 5 = 15$

Notemos que el resultado fue el mismo sin importar la fórmula que utilizáramos.

Cálculo del módulo y ángulos de vectores

Como vimos anteriormente, existen dos fórmulas equivalentes para calcular el producto escalar de dos vectores. Por lo tanto, se puede utilizar el producto escalar para calcular el módulo de un vector o el ángulo entre dos vectores.

Calcular el módulo de un vector utilizando el producto escalar

Notemos que si $\vec{u}$ es un vector, entonces

$\displaystyle \vec{u} \cdot \vec{u} = \left| \vec{u} \right| \cdot \left| \vec{u} \right| \cos\left( 0^{\circ} \right) = \left| \vec{u} \right|^2$

Por lo tanto,

$\displaystyle \left| \vec{u} \right| = \sqrt{\vec{u} \cdot \vec{u}} = \sqrt{u_1^2 + u_2^2}$

Esta fórmula se puede utilizar para calcular el módulo de un vector $\vec{u}$ utilizando el producto escalar de $\vec{u}$ consigo mismo.

Calcular el ángulo entre dos vectores utilizando el producto escalar

Supongamos que tenemos los vectores $\vec{u} = (u_1, u_2)$ y $\vec{v} = (v_1, v_2)$ . Entonces

$\displaystyle \vec{u} \cdot \vec{v} = \left| \vec{u} \right| \left| \vec{v} \right| \cos \alpha$

Despejando $\cos \alpha$ , tenemos

$\displaystyle \cos \alpha = \frac{\vec{u} \cdot \vec{v}}{\left| \vec{u} \right| \left| \vec{v} \right|}$

Así, si sustituimos la otra fórmula del producto escalar, se tiene

$\displaystyle \cos \alpha = \frac{u_1 v_1 + u_2 v_2}{\sqrt{u_1^2 + u_2^2} \sqrt{v_1^2 + v_2^2} }$

Esta fórmula se utiliza para calcular $\alpha$ utilizando la función arco-coseno.

Ejemplos

1 Consideremos, nuevamente, los vectores $\vec{u} = (3, 0)$ y $\vec{v} = (5, 5)$ . Entonces el módulo de estos vectores es:

$\displaystyle \left| \vec{u} \right| = \sqrt{ \vec{u} \cdot \vec{u} } = \sqrt{9} = 3$

$\displaystyle \left| \vec{v} \right| = \sqrt{ \vec{v} \cdot \vec{v} } = \sqrt{50} = 5\sqrt{2}$

2 Ahora calcularemos el ángulo entre $\vec{u} = (3, 0)$ y $\vec{v} = (5, 5)$ . Tenemos que

$\displaystyle \cos \alpha = \frac{3 \cdot 5 + 0 \cdot 5}{\sqrt{3^2 + 0^2} \sqrt{5^2 + 5^2} } = \frac{15}{3 \cdot 5\sqrt{2}} = \frac{1}{\sqrt{2}}$

De manera que

$\displaystyle \cos \alpha = \frac{1}{\sqrt{2}}$

Por lo tanto, debemos tener que

$\displaystyle \alpha = 45^{\circ}$

Ortogonalidad de dos vectores

Sabemos que dos vectores son ortogonales (o perpendiculares) si el ángulo entre ellos es $\alpha = 90^{\circ}$ o $\alpha = -90^{\circ}$ . En cualquiera de estos casos, tenemos que $\cos \alpha = 0$ . Por lo tanto, si dos vectores son ortogonales, se tiene que

$\displaystyle \vec{u} \cdot \vec{v} = \left| \vec{u} \right| \left| \vec{v} \right| \cos \alpha = 0$

Es decir, dos vectores $\vec{u} \neq 0$ y $\vec{v} \neq 0$ serán ortogonales siempre que se cumpla que

$\displaystyle \vec{u} \cdot \vec{v} = u_1 v_1 + u_2 v_2 = 0$

Ejemplo

Verificaremos la ortogonalidad de los vectores $\vec{u} = (3, 0)$ y $\vec{v} = (5, 5)$ que utilizamos en los ejemplos anteriores. Observemos que

$\displaystyle \vec{u} \cdot \vec{v} = 3 \cdot 5 + 0 \cdot 5 = 15 \neq 0$

Por lo tanto, los vectores $\vec{u}$ y $\vec{v}$ no son perpendiculares.

Interpretación geométrica del producto escalar

Notemos que $\left| \vec{u} \right| \cos \alpha$ se puede ver como el módulo de la proyección del vector $\vec{u}$ sobre $\vec{v}$ —siempre que $-90^{\circ} \leq \alpha \leq 90^{\circ}$ —, tal y como se muestra en la siguiente figura. La proyección sería el vector con origen $O$ y extremo $A'$ .

reopresentacion grafica de una proyeccion de un vector sobre otro

Eso se sigue al observar el triángulo rectángulo que se formó en la figura anterior. Sabemos que

$\displaystyle \cos \alpha = \frac{\text{\text{CA}}}{\text{HI}} = \frac{\overline{OA'}}{\left| \vec{u} \right|}$

De manera que, al despejar $\overline{OA'}$ , tenemos

$\displaystyle \overline{OA'} = \left|\vec{u} \right| \cos \alpha$

Para imaginar la proyección, piensa que hay una fuente de luz y la proyección es la sombra del vector $\vec{u}$ sobre el vector $\vec{v}$ . Además, esta fuente de luz debe estar colocada de tal forma que un vector perpendicular a $\vec{v}$ no proyecte sombra alguna. Observa la siguiente figura:

De este modo, el producto $\left| \vec{u} \right| \left| \vec{v} \right| \cos \alpha$ puede verse como el módulo de uno de los vectores multiplicado por el módulo de la proyección del otro vector. Es decir, al sustituir $\overline{OA'} = \left|\vec{u} \right| \cos \alpha$ en la fórmula del producto escalar, tenemos

$\displaystyle \vec{u} \cdot \vec{v} = \left| \vec{v} \right| \cdot \overline{OA'}$

Por lo tanto, podemos calcular el módulo de la proyección del vector $\vec{u}$ sobre el vector $\vec{v}$ utilizando

$\displaystyle \overline{OA'} = \frac{\vec{u} \cdot \vec{v} }{\left| \vec{v} \right| }$

Nota: Si tenemos que $\left| \vec{u} \right| \cos \alpha$ es negativo, entonces esto significa que la proyección tiene sentido contrario al vector $\vec{v}$ . Esto ocurre cuando $\text{[math]}$ 90^{\circ}»> o <img class="ql-img-inline-formula lazyloaded" title="Rendered by QuickLaTeX.com" src="https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-cc7d00908baea38a0ed703b6e26ea94c_l3.png" alt="\alpha . En este caso, el módulo de la proyección está dada por $| \overline{OA'} |$ . Observa la siguiente figura:

Ejemplo

Encontraremos la proyección de $\vec{u} = (2, 1)$ sobre el vector $\vec{v} = (-3, 4)$ . Para hacer esto, calculemos

$\displaystyle P(\vec{u}, \vec{v}) = \frac{2 \cdot (-3) + 1 \cdot 4}{\sqrt{(-3)^2 + 4^2}} = -\frac{2}{5}$

Observemos que $P(\vec{u}, \vec{v})$ tiene signo negativo. Por lo tanto, la proyección tiene sentido contrario que $\vec{v}$ y su módulo es $2/5$ . Observa la siguiente figura:

Propiedades del producto escalar

El producto escalar satisface diferentes propiedades. Las más importantes son las siguientes:

1 El producto escalar es conmutativo. En otras palabras, «el orden de los factores no altera el producto». De este modo, no importa en qué orden se multipliquen los vectores.

$\displaystyle \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$

2 Asociatividad respecto a la multiplicación por escalar. Es decir, si multiplicamos $\vec{u}$ por $\vec{v}$ y luego por un escalar $k$ , entonces el resultado es lo mismo que realizar primero $k\vec{u}$ y luego hacer el producto escalar por $\vec{v}$ . Esto es,

$\displaystyle k \left(\vec{u} \cdot \vec{v} \right) = \left(k\vec{u} \right) \cdot \vec{v}$

3 Distributividad respecto a la suma. Esto es,

$\displaystyle \left(\vec{u} + \vec{v} \right) \cdot \vec{w} =\vec{u} \cdot \vec{w} + \vec{v} \cdot \vec{w}$

Nota: Las propiedades 2 y 3 juntas se conocen como linealidad del producto escalar respecto al primer operando.

Nota: Debido a que el producto escalar es conmutativo, entonces también se cumple la linealidad respecto al segundo operando. Es decir,

$\displaystyle k \left(\vec{u} \cdot \vec{v} \right) = \vec{u} \cdot \left(k\vec{v} \right)$

$\displaystyle \vec{u} \cdot \left(\vec{v} + \vec{w} \right) =\vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$

4 El producto escalar es definido positivo. Esto es, el producto escalar de un vector no nulo por sí mismo siempre es positivo.

$\displaystyle \vec{u} \neq 0 \quad \Rightarrow \quad \vec{u} \cdot \vec{u} \geq 0$

Elementos de un vector

Módulo de un vector a partir de sus componentes

Módulo a partir de las coordenadas de los puntos:

Clases de vectores

Suma de vectores

Interpretación gráfica de la suma

Regla del paralelogramo

Resta de vectores

Producto de vector por escalar

Ejemplos de ejercicios con vectores

Definición y propiedades

Ejemplos

Vectores linealmente dependientes

Propiedades

Vectores linealmente independientes

¿Como se forma la base de dos vectores?

Clasificación de bases

Base ortogonal

Base ortonormal

1

2

Coordenadas del punto medio de un segmento

Condición para que tres puntos estén alineados

Simétrico de un punto respecto de otro

Coordenadas del baricentro

División de un segmento en una relación dada

Maneras de calcular el producto escalar

Ejemplos

Cálculo del módulo y ángulos de vectores

Calcular el módulo de un vector utilizando el producto escalar

Calcular el ángulo entre dos vectores utilizando el producto escalar

Ejemplos

Ortogonalidad de dos vectores

Ejemplo

Interpretación geométrica del producto escalar

Ejemplo

Propiedades del producto escalar

Comparte esto: