TEORÍA ESTADÍSTICA.

Definición de Estadística

La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.

Un estudio estadístico consta de las siguientes fases:

1º Recogida de datos

2º Organización y representación de datos

3º Análisis de datos

4º Obtención de conclusiones

Conceptos de Estadística

Población

Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.

Ejemplo: El conjunto de los ciudadanos españoles.

Individuo

Un individuo o unidad estadística es cada uno de los elementos que componen la población.

Ejemplo: Un ciudadano español.

Muestra

Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.

Ejemplo: Ciudadanos españoles mayores de edad.

Muestreo

El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.

Valor

Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico.

Ejemplo: Si lanzamos una moneda al aire veces obtenemos dos valores: cara y cruz.

Dato

Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico.

Ejemplo: Si lanzamos una moneda al aire veces obtenemos datos: cara, cara, cruz, cara, cruz.

Variables estadísticas

¿Qué es una variable estadística?

Una variable estadística es cada una de las características o cualidades que poseen los individuos de una población.

Tipos de variable estadísticas

Variables cualitativas

Las variables cualitativas se refieren a características o cualidades que no pueden ser medidas con números. Podemos distinguir dos tipos:

1º Variable cualitativa nominal

Una variable cualitativa nominal presenta modalidades no numéricas que no admiten un criterio de orden.

Ejemplo:

El estado civil, con las siguientes modalidades: soltero, casado, separado, divorciado y viudo.

2º Variable cualitativa ordinal o variable cuasicuantitativa

Una variable cualitativa ordinal presenta modalidades no numéricas, en las que existe un orden.

Ejemplos:

La nota en un examen: suspenso, aprobado, notable, sobresaliente.
Puesto conseguido en una prueba deportiva: primero, segundo, tercer, …
Medallas de una prueba deportiva: oro, plata, bronce.

Variables cuantitativas

Una variable cuantitativa es la que se expresa mediante un número, por tanto se pueden realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:

1º Variable discreta

Una variable discreta es aquella que solo puede tomar un número finito de valores entre dos valores cualesquiera de una característica.

Ejemplo:

El número de hermanos de amigos: 2, 1, 0, 1, 3 .

2º Variable continua

Una variable continua es aquella que puede tomar un número infinito de valores entre dos valores cualesquiera de una característica.

Ejemplos:

La altura de los amigos: 1.73, 1.82, 1.77, 1.69, 1.75

Construcción de tablas de frecuencia

Definición de distribución de frecuencias

La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.

Frecuencia absoluta

La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.

Al tirar una moneda veces salen caras

Se representa por f_i , aunque otros autores la representan como n_i .

La suma de las frecuencias absolutas es igual al número total de datos, que se representa por .

Para indicar resumidamente estas sumas se utiliza la letra griega (sigma mayúscula) que se lee suma o sumatoria.

Frecuencia relativa

La frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos.

Se puede expresar en tanto por ciento y se representa por .

La frecuencia relativa es un número comprendido entre y .

La suma de las frecuencias relativas es igual a .

\displaystyle n cara+n cruz= \frac {35}{50}+ \frac {15}{50}= \frac {50}{50}=1

Frecuencia acumulada

La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado.

Se representa por F_i .

Frecuencia relativa acumulada

La frecuencia relativa acumulada es el cociente entre la frecuencia acumulada de un determinado valor y el número total de datos.

Se puede expresar en tantos por ciento.

Ejemplo:

Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:

32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32,
31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29 .

En la primera columna de la tabla colocamos la variable ordenada de menor a mayor

En la segunda hacemos el recuento

En la tercera anotamos la frecuencia absoluta

En la cuarta anotamos la frecuencia acumulada:

En la primera casilla colocamos la primera frecuencia absoluta: F_i=f_i

En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente:

En la tercera casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente:

La última tiene que ser igual a (sumatoria de f_i ).

En la quinta columna disponemos las frecuencias relativas (n_i) que son el resultado de dividir cada frecuencia absoluta por N (31)

En la sexta anotamos la frecuencia relativa acumulada N_i .

En la primera casilla colocamos la primera frecuencia relativa acumulada.

En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa correspondiente y así sucesivamente hasta la última, que tiene que ser igual a .

Este tipo de tablas de frecuencias se utiliza con variables discretas.

Distribución de frecuencias agrupadas

La distribución de frecuencias agrupadas o tabla con datos agrupados se emplea si las variables toman un número grande de valores o la variable es continua.

Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.

Límites de la clase

Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.

Amplitud de la clase

La amplitud de la clase es la diferencia entre el límite superior e inferior de la clase.

Marca de clase

La marca de clase es el punto medio de cada intervalo y es el valor que representa a todo el intervalo para el cálculo de algunos parámetros.

La marca de clase se representa por c_i

Construcción de una tabla de datos agrupados

3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13

1º Se localizan los valores menor y mayor de la distribución. En este caso son y .

2º Se restan y se busca un número entero un poco mayor que la diferencia y que sea
divisible por el número de intervalos queramos establecer.

Es conveniente que el número de intervalos oscile entre y .

En este caso, 48 - 3 = 45 , incrementamos el número hasta , $50 \div 5 = 10$ intervalos.

Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.

c_i es la marca de clase que es el punto medio de cada intervalo.

Diagrama de barras y polígonos de frecuencias

Diagrama de barras

Un diagrama de barras se utiliza para representar datos cualitativos o datos cuantitativos de tipo discreto.

Se representan sobre unos ejes de coordenadas, en el eje de abscisas se colocan los valores de la variable, y sobre el eje de ordenadas las frecuencias absolutas o relativas o acumuladas.

Los datos se representan mediante barras de una altura proporcional a la frecuencia.

Ejemplo:

Un estudio hecho al conjunto de los 20 alumnos de una clase para determinar su grupo sanguíneo ha dado el siguiente resultado:

Grupo sanguíneo	f_i
A	6
B	4
AB	1
0	9
	20

Representa lo anterior mediante un diagrama de barras.

1º En el eje de las abscisas colocamos los elemento del grupo sanguíneo y en el eje de las ordenadas la frecuencias de cada elemento.

2º Representamos cada elemento del grupo sanguíneo con una barra. Todas las barras deben tener el mismo ancho.

3º Obtenemos la siguiente gráfica

Polígonos de frecuencia

Un polígono de frecuencias se forma uniendo los extremos de las barras mediante segmentos.

También se puede realizar trazando los puntos que representan las frecuencias y uniéndolos mediante segmentos.

Ejemplo:

Las temperaturas en un día de otoño de una ciudad han sufrido las siguientes variaciones:

Hora	Temperatura
6	7º
9	12°
12	14°
15	11°
18	12°
21	10°
24	8°

Representa lo anterior mediante un polígono de frecuencias.

1º En el eje de las abscisas colocamos las horas y en el eje de las ordenadas las temperaturas.

2º Trazamos para cada hora de la tabla su respectiva frecuencia.

3º Obtenemos la siguiente gráfica

Como hacer un diagrama de sectores

En un diagrama de sectores los datos se representan en un círculo dividido en sectores, de modo que el ángulo de cada sector es proporcional a la frecuencia absoluta correspondiente.

{\alpha=\displaystyle\frac{360^{o}}{N}\cdot f_{i}}

El diagrama de sectores se construye con la ayuda de un transportador de ángulos.

Un diagrama de sectores se puede utilizar para todo tipo de variables, pero se usa frecuentemente para las variables cualitativas.

Ejemplo:

En una clase de alumnos, juegan a baloncesto, practican la natación, juegan al fútbol y el resto no practica ningún deporte.Representar los datos en un diagrama de vectores.

1º Calculamos el ángulo correspondiente aplicando regla de tres directa

2º Representamos los sectores con sus ángulos correspondientes

El histograma

¿Qué es un histograma?

Un histograma es la representación gráfica en forma de barras, que simboliza la distribución de un conjunto de datos. Sirven para obtener una «primera vista» general, o panorama, de la distribución de la población, o de la muestra, respecto a una característica, cuantitativa y continua.

En un histograma el eje de las $\qquad x \qquad$ (o abscisas) consiste del rango en el cual se encuentran los datos. Ahora, las bases de los rectángulos consisten de los intervalos en los cuales agrupamos dichos datos.

Por otro lado, en el eje de las $\qquad y \qquad$ (u ordenadas) tenemos más opciones, dependiendo estas opciones es el tipo de histograma que tenemos. Los dos tipos principales de histogramas son los siguientes:

Histograma de frecuencias absolutas. Representa la frecuencia absoluta mediante la altura de las barras.
Histograma de frecuencias relativas.Representa la frecuencia relativa mediante la altura de las barras.

Así, ya que conocemos las características de un histograma, tenemos que para construir uno, dado un conjunto de datos, debemos seguir los siguientes pasos.

Dibujamos el eje de las abscisas de tal forma que incluya como mínimo el rango de los datos y, posteriormente, dividimos este rango en los intervalos dados.
Dibujamos el eje de las ordenadas representando las frecuencias absolutas o relativas según sea el caso.
Se dibujan los rectángulos de anchura igual y proporcional al intervalo (en nuestro caso todos tendrán la misma anchura) y de altura igual a la frecuencia absoluta o relativa, según sea el caso.

Ejemplo. Consideremos los siguientes datos

Nuestro histograma de frecuencias absolutas sería el siguiente

Por otro lado, nuestro histograma de frecuencias relativas sería el siguiente

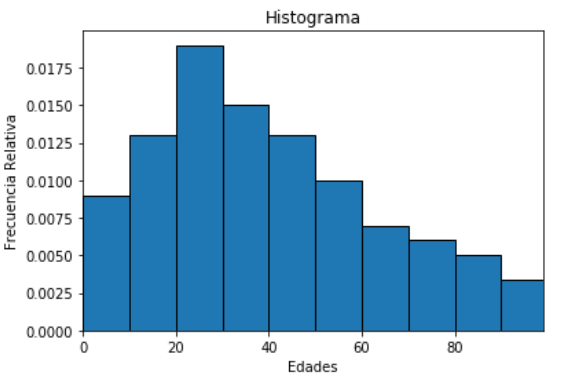
Polígono de frecuencia

Un polígono de frecuencias da la misma información de un histograma, para esto graficamos un punto por cada clase del conjunto de datos en donde en la entrada de las abscisas se toma el valor del punto medio de la clase y en la entrada las ordenadas tendrán en mismo valor que la altura del rectángulo. Al final, unimos cada punto con su sucesor y su antecesor.

Ejemplo. Utilizando el mismo conjunto de datos del ejemplo anterior

Histograma y polígono de frecuencias acumuladas

Si se representan las frecuencias acumuladas de una tabla de datos agrupados se obtiene el histograma de frecuencias acumuladas y su correspondiente polígono.

Ejemplo. Utilizando el mismo conjunto de datos del ejemplo anterior

Histogramas con intervalos de amplitud diferente

En este caso, el histograma debería representar la frecuencia de cada intervalo con el área de la barra y no con su altura. Por lo tanto, calculamos la altura de cada barra de la siguiente manera

En donde

es la altura del intervalo
es la frecuencia absoluta o relativa del intervalo, según sea el caso.
es la amplitud del intervalo

La idea del polígono de frecuencias sigue siendo exactamente la misma.

Ejemplo. Consideremos una agrupación distinta de los datos de los ejemplos anteriores

Su histograma y su polígono de frecuencias relativas sería el siguiente

Parámetros estadísticos descriptivos

Un parámetro estadístico es un número que se obtiene a partir de los datos de una muestra estadística. Los parámetros estadísticos también se conocen como estadísticos descriptivos.

Los parámetros estadísticos sirven para sintetizar o resumir la información dada por una tabla o por una gráfica. En otras palabras, dados unos pocos parámetros estadísticos se puede tener una idea general de la distribución de la información.

Los parámetros estadísticos dan un buen resumen cuando se conoce la distribución de la población. En particular, si la muestra proviene de una distribución normal, entonces el promedio típico y la desviación estándar dan un buen resumen de la distribución.

Ejemplos de parámetros estadísticos son el promedio, la mediana, la desviación estándar o los cuartiles.

Los parámetros estadísticos se clasifican según la información que resumen. Los dos tipos más comunes de parámetros estadísticos son:

De tendencia central
De dispersión

Otros tipo de parámetros estadísticos son aquellos de forma y escala. Estos parámetros son más utilizados en distribuciones como la Beta, Pareto o Weibull —por lo tanto, no las describiremos ya que nos enfocamos principalmente en la distribución normal—.

Medidas de tendencia central

Estos parámetros nos indican alrededor de qué valor (centro) se distribuyen los datos.

Algunas medidas de tendencia central son (al dar clic en el enlace podrás ver una descripción detallada de cada parámetro):

Media aritmética:

La media es el valor promedio de la muestra. También se puede interpretar como el centro de gravedad de los datos.

Mediana:

La mediana es el valor que separa la mitad superior de la muestra y la inferior. En otras palabras, divide los datos en dos partes iguales.

Moda:

La moda es el valor que más se repite en una muestra. Es decir, es el valor más frecuente.

Ejemplo

Tenemos los siguientes datos, los cuales representan las edades en una oficina:

21, 24, 29, 43, 38, 27, 31, 27, 27, 26, 34, 23, 39

Para estos datos:

1º Su media es 29.92 años. Es decir, el trabajador promedio tiene 30 años (después de redondear).

2º La moda de estos datos es 27 años. Por lo tanto, 27 años es la edad más frecuente.

3º La mediana es 27 años también. Esto significa que la mitad de los empleados tienen más de 27 años, mientras que la otra mitad tienen 27 años o menos.

Podemos observar los datos en la siguiente gráfica:

Medidas de dispersión

Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución. Es decir, son un resumen sobre qué tan dispersos están los datos.

Algunas medidas de dispersión son:

Rango o recorrido:

El rango es la diferencia entre el mayor y el menor de los valores de una muestra. Este valor nos indica en qué rango se encuentran los datos.

Desviación media:

La desviación media es la media de los valores absolutos de las desviaciones respecto a la media. En otras palabras, es el promedio de cuánto se desvían los datos de la media (en valor absoluto).

Varianza:

La varianza es el promedio del cuadrado de las desviaciones respecto a la media. O sea, mide el promedio de cuánto se desvían los datos al cuadrado —primero elevamos al cuadrado y luego calculamos el promedio—.

Desviación estándar:

La desviación estándar es la raíz cuadrada de la varianza. Este suele ser un mejor estimador que la desviación media cuando tratamos con la distribución normal.

Cuantiles:

Los cuantiles dividen una muestra en partes iguales. Estos nos ayudan a tener una idea de los rangos en los que se concentran más valores.

Dependiendo el valor de , los cuartiles pueden tener nombres particulares:

Cuartiles: Estos dividen los datos en cuatro partes iguales.
Deciles: Los deciles dividen la muestra en diez conjuntos del mismo tamaño.
Percentiles: Los percentiles dividen los datos en cien partes iguales.

Ejemplo

Con los mismos datos del ejemplo anterior —edades de los empleados de una oficina—:

La medidas de dispersión de estos datos son:

1º Su rango es 22 años. Es decir, entre el trabajador más joven y el empleado más grande hay 22 años de diferencia.

2º Su desviación media es 5.44 años. Esto es, los empleados suelen estar 5 años más jóvenes o más viejos que la media —esta desviación es promedio, por lo tanto, algunos empleados se desvían más de 5 años y otros se desvían menos de 5 años—.

3º La varianza 41.61 años.

4º La desviación estándar es de 6.45 años.

5º Por último, la muestra tiene solo 13 individuos. Por este motivo, no es apropiado utilizar deciles o percentiles. Sin embargo, podemos calcular los cuartiles:

Primer cuartil: 26 años.
Segundo cuartil: 27 años.
Tercer cuartil: 34 años.

De esta manera, podemos interpretar que aproximadamente el 25% de los empleados tienen menos de 26 años. Además, hay muchos empleados entre 26 y 27 años (casi el 25% de los empleados tienen esas edades, pues están entre el primer y segundo cuartil). Por último, sólo el 25% de los trabajadores tienen más de 34 años —que es equivalente a decir que aproximadamente el 75% de los trabajadores son menores de 34 años—.

Moda estadística

Definición de moda estadística

La moda es el valor que tiene mayor frecuencia absoluta.
Se representa por _.
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, entonces la distribución es bimodal (en caso de que sean valores) o multimodal (en caso de que existan mas de ), es decir, tiene varias modas.
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
Se puede hallar la moda para variables cualitativas y cuantitativas.
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.Ejemplos de ejercicios de moda

Ejemplos de cálculo de la moda

1º Hallar la moda de la distribución: 2, 3, 3, 4, 4, 4, 5, 5

2º Hallar la moda de la distribución: 1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9

3º Hallar la moda de la distribución: 2, 2, 3, 3, 6, 6, 9, 9

Como todas las puntuaciones del grupo tienen la misma frecuencia, no hay moda.

4º Hallar la moda de la distribución: 0, 1, 3, 3, 5, 5, 7, 8

Cálculo de la moda para datos agrupados

Caso 1: Cuando todos los intervalos tienen la misma amplitud.

\displaystyle M_o=L_i+\frac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot a_i

es el límite inferior de la clase modal
es la frecuencia absoluta de la clase modal
$f_{i-1}$ es la frecuencia absoluta inmediatamente inferior a la clase modal
$f_{i+1}$ es la frecuencia absoluta inmediatamente posterior a la clase modal
es la amplitud de la clase

También se utiliza otra fórmula de la moda que da un valor aproximado de ésta:

\displaystyle M_o=L_i+\frac{f_{i+1}}{f_{i-1}+f_{i+1}}\cdot a_i

Ejemplo:

Calcular la moda de una distribución estadística que viene dada por la siguiente tabla:

En primer lugar buscamos el intervalo donde se encuentra la moda, que será el intervalo que tenga la mayor frecuencia absoluta (f_i) .

La clase modal es: [66, 69)

Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos:

Límite inferior:

\displaystyle M_o=66+\frac{(42-18)}{(42-18)+(42-27)}\cdot 3=67.846

\displaystyle M_o=66+\frac{27}{18+27}\cdot 3=67.8

Caso 2: Cuando los intervalos tienen amplitudes distintas.

1º En primer lugar tenemos que hallar las alturas.

2º La clase modal es la que tiene mayor altura.

\displaystyle M_o=L_i+\frac{h_i-h_{i-1}}{(h_i-h_{i-1})+(h_i-h_{i+1})}\cdot a_i

3º La fórmula de la moda aproximada cuando existen distintas amplitudes es:

\displaystyle M_o=L_i+\frac{h_{i+1}}{h_{i-1}+h_{i+1}}\cdot a_i

Ejemplo:

En la siguiente tabla se muestra las calificaciones (suspenso, aprobado, notable y sobresaliente) obtenidas por un grupo de 50 alumnos. Calcular la moda.

En primer lugar creamos una nueva columna con las alturas, dividiendo las frecuencias absolutas entre las amplitudes de los intervalos correspondientes:

\displaystyle h_1=\frac{15}{5}=3 \ \ \ \ \ \ \ \ \ \ h_2=\frac{20}{2}=10

\displaystyle h_3=\frac{12}{2}=6 \ \ \ \ \ \ \ \ \ \ h_4=\frac{3}{1}=3

La clase modal es [5, 7) porque es la que tiene mayor altura

Limite inferior:

\displaystyle M_o=5+\frac{(10-3)}{(10-3)+(10-6)}\cdot 2=6.27

\displaystyle M_o=5+\frac{6}{3+6}\cdot 2=6.33

La mediana

¿Qué es la mediana?

La mediana es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.

La mediana se representa por M_e

La mediana se puede hallar solo para variables cuantitativas.

Ejemplo de cálculo simple de la mediana

1º Ordenamos los datos de menor a mayor.

2º Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma

3º Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.

\displaystyle M_e=\frac{9+10}{2}=\frac{19}{2}=9.5

Fórmula y cálculo de la mediana para datos agrupados

La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.

Es decir tenemos que buscar el intervalo en el que se encuentre.

\displaystyle M_e=L_{i}+\cfrac{\cfrac{N}{2}-F_{i-1}}{f_{i}}\cdot a_{i}

$L_{i}$ es el límite inferior de la clase donde se encuentra la mediana

$\cfrac{N}{2}$ es la semisuma de las frecuencias absolutas

$f_{i}$ es la frecuencia absoluta de la clase mediana

$F_{i-1}$ es la frecuencia acumulada anterior a la clase mediana

$a_{i}$ es la amplitud de la clase

La mediana es independiente de las amplitudes de los intervalos

Ejemplo de cálculo de la mediana para distribución estadística

Calcular la mediana de una distribución estadística que viene dada por la siguiente tabla:

En primer lugar crearemos una nueva columna con los valores de la frecuencia acumulada:

En la primera casilla colocamos la primera frecuencia absoluta. En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a N(100)

Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la por porque la mediana es el valor central

Buscamos en la columna de las frecuencias acumuladas $(F_{i})$ el intervalo que contiene a

Clase de la mediana: [66,69)

Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:

M_e=66+\cfrac{\cfrac{100}{2}-23}{42}\cdot 3 = 67,92

La media aritmética

Definición

La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos. Denotamos la media con el símbolo $\overline{X}$ y la calculamos de la siguiente manera

\begin{align*} \overline{X} &= \frac{x_1 + x_2 + \cdots + x_N}{N}\\ &= \frac{\sum_{i=1}^{N}{x_i}}{N}\\ \end{align*}

en donde cada x_i representa uno de nuestros datos y es el número total de datos que tenemos.

Ejemplo:

Los pesos de seis amigos son: 84, 91, 72, 68, 87 y $78 \; \text{kg}$ .

Hallar el peso medio.

Primero, notemos que tenemos seis datos, por lo tanto, N = 6 . Procedamos a calcular la media

\begin{align*} \overline{X} &= \frac{84 + 91 + 72 + 68 + 87 + 78}{6}\\ &= \frac{480}{6}\\ &= 80 \end{align*}

Media aritmética para datos agrupados

Cuando los datos vienen agrupados en una tabla de frecuencias, la expresión de la
media es distinta. Supongamos que tenemos clases diferentes en nuestra tabla de frecuencias, en donde para cada clase C_i , tenemos su media x_i y su frecuencia f_i correspondiente, entonces calculamos la media como:

\begin{align*} \overline{X} &= \frac{x_1 \cdot f_1 + x_2 \cdot f_2 + \cdots + x_K \cdot f_K}{f_1 + f_2 + \cdots + f_K}\\ &= \frac{\sum_{i=1}^{K}{x_i \cdot f_i}}{\sum_{j=1}^{K}{f_j}}\\ &= \frac{\sum_{i=1}^{K}{x_i \cdot f_i}}{N}\\ \end{align*}

Debemos observar que ahora es la suma de las frecuencias de cada clase, esto es

$N = \sum_{j=1}^{K}{f_j}$ .

Además, cuando cada grupo o clase es un intervalo, la media de dicho intervalo es simplemente el punto medio entre los límites, así, suponiendo que un grupo es el intervalo (a, b) , entonces su media es $\frac{a + b}{2}$ .

Como observación a considerar, notemos que al tener una tabla de frecuencias, al agrupar los datos, sustituimos cada dato por la media del grupo o clase al que pertenece, y que la suma de todas las frecuencias es igual a la cantidad de datos que tendríamos si no agrupáramos, por lo tanto, al calcular la media en datos agrupados, lo que hacemos es simplemente reemplazar cada dato por la media del grupo o clase al que pertenece. En caso de tener datos no agrupados, en general es mejor no agrupar ya que esto implica pérdida de información.

Ejercicio de media aritmética para datos agrupados

En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones
que muestra la tabla.

Calcula la puntuación media.

Podemos observar como cada x_i es punto medio del correspondiente intervalo.

Para obtener la media, en primer lugar, vamos a calcular la sumatoria de , crearemos una nueva columna para los productos de la variable con su correspondiente frecuencia absoluta y lo sumaremos todo. También tenemos que calcular que es la sumatoria de las frecuencias absolutas.

Entonces, utilizando nuestros datos, la media está dada por

\begin{align*} \overline{X} &= \frac{\sum_{i=1}^{7}{x_i \cdot f_i}}{\sum_{j=1}^{7}{f_j}}\\ &= \frac{\sum_{i=1}^{7}{x_i \cdot f_i}}{N}\\ &= \frac{1820}{42}\\ &= 43.33 \end{align*}

Propiedades de la media aritmética

Primero, una definición que nos ayudará a entender mejor las definiciones. Sea $x_1, x_2, \cdots x_N$ un conjunto de datos y $\overline{X}$ la media de los datos, entonces, definimos la desviación de un dato, x_i , respecto a la media como

$\qquad x_i - \overline{X}\qquad$ .

1. La suma de las desviaciones de todos los datos de una distribución
respecto a la media de la misma igual a cero. Esto es

\displaystyle \sum_{i= 1}^{N}{(x_i - \overline{X})} = \sum_{i= 1}^{N}{(\overline{X} - x_i)} = 0

La suma de las desviaciones de los números 8, 3, 5, 12, 10 de su media aritmética 7.6 es igual a :

\begin{align*} \sum_{i= 1}^{5}{(x_i - \overline{X})} &= (8-7.6) + (3-7.6) + (5-7.6)\\ &+ (12-7.6) + (10 -7.6)\\ &= 0.4 - 4.6 - 2.6 + 4.4 + 2.4\\ &= 0 \end{align*}

2. La suma de los cuadrados de las desviaciones de los valores de la variable con respecto a un número cualquiera se hace mínima cuando dicho número coincide con la media aritmética. En otras palabras, lo siguiente siempre se cumple

\displaystyle \sum_{i= 1}^{N}{(x_i - \overline{X})^2} \leq \sum_{i= 1}^{N}{(x_i - a)^2}, \qquad a \in \mathbb{R}.

3. Si a todos los valores de la variable se les suma un mismo número, la media aritmética de estos nuevos datos es a la media de los anteriores más la misma cantidad que se le sumó a los datos. Esto es, suponiendo que tenemos los datos $x_1, x_2, \dots, x_N$ con media $\overline{X}$ , ahora, si le sumamos a todos los datos una cantidad , $x_1 + a, x_2 + a, \dots, x_N + a$ , la media de estos nuevos datos es

\displaystyle \overline{X_a} = \overline{X} + a

4. Si todos los valores de la variable se multiplican por un mismo número la media
aritmética queda multiplicada por dicho número. Esto es, suponiendo que tenemos los datos $x_1, x_2, \dots, x_N$ con media $\overline{X}$ , ahora, si multiplicamos a todos los datos por una cantidad , $x_1 \cdot a, x_2 \cdot a, \dots, x_N \cdot a$ , la media de estos nuevos datos es

\displaystyle \overline{X_a} = \overline{X} \cdot a

Observaciones sobre la media aritmética

1. La media se puede hallar sólo para variables cuantitativas.

2. La media es independiente de las amplitudes de los intervalos.

3. La media es muy sensible a las puntuaciones extremas, también conocidos como valores atípicos. Si tenemos una distribución con los siguientes pesos:

$65 \; \text{kg}, 69 \; \text{kg}, 65 \; \text{kg}, 72 \; \text{kg}, 66 \; \text{kg}, 75 \; \text{kg}, 70 \; \text{kg}, 110 \; \text{kg}$ .

La media es igual a $74 \; \text{kg}$ , que es una medida de centralización poco representativa
de la distribución, sin embargo esto pasa porque tenemos un dato muy alejado a los demás, 110 .

4. La media no se puede calcular si hay un intervalo con una amplitud indeterminada.

En este caso no es posible hallar la media porque no podemos calcular la marca de clase de último intervalo.

Cuartil

¿Que son los cuartiles?

Los cuartiles son una herramienta que usamos en la estadística y que nos sirve para administrar grupos de datos previamente ordenados.

Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.

Q_1, Q_2 y Q_3 determinan los valores correspondientes al %, al % y al % de los datos. Q_2 coincide con la mediana.

Cálculo de los cuartiles

1. Ordenamos los datos de menor a mayor.

2.Buscamos el lugar que ocupa cada cuartil mediante la expresión $\displaystyle \frac{k \cdot N}{4}=1,2,3$

Número impar de datos

Número par de datos

Cálculo de los cuartiles para datos agrupados

En primer lugar buscamos la clase donde se encuentra $\displaystyle \frac{k \cdot N}{4}=1,2,3$ , en la tabla de las frecuencias acumuladas.

Q_k=L_i+\frac{\frac{k \cdot N}{4}-F_{i-1}}{f_i}\cdot a_i \ \ \ \ \ \ \ \ \ \ k=1, 2, 3

L_i es el límite inferior de la clase donde se encuentra el cuartil.

es la suma de las frecuencias absolutas.

$F_{i-1}$ es la frecuencia acumulada anterior a la clase del cuartil.

a_i es la amplitud de la clase.

Ejemplo de ejercicio de cuartiles

Calcular los cuartiles de la distribución de la tabla:

En primer lugar crearemos una nueva columna con los valores de la frecuencia acumulada:

En la primera casilla colocamos la primera frecuencia absoluta.

En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a N = 65

Cálculo del primer cuartil

Buscamos el intervalo donde se encuentra el primer cuartil, multiplicando por N = 65 y dividiendo por .

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 16.25 .

La clase de Q_1 es: [60, 70)

Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:

\displaystyle Q_1=60+\frac{16.25-8}{10}\cdot 10=68.25

Cálculo del segundo cuartil

Buscamos el intervalo donde se encuentra el segundo cuartil, multiplicando por N = 65 y dividiendo por .

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 32.5 .

La clase de Q_2 es: [70, 80)

Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:

\displaystyle Q_2=70+\frac{32.5-18}{16}\cdot 10=79.0625

Cálculo del tercer cuartil

Buscamos el intervalo donde se encuentra el tercer cuartil, multiplicando por N = 65 y dividiendo por .

\displaystyle \frac{65 \cdot 3}{4}=48.75

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 48.75

La clase de Q_3 es: [90, 100)

Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:

\displaystyle Q_3=90+\frac{48.75-48}{10}\cdot 10=90.75

Deciles

Definición de deciles

Los deciles son los nueve valores que dividen una serie de datos ordenados en diez partes iguales.

Los deciles dan los valores correspondientes al %, al %… y al % de los datos.

El quinto decil coincide con la mediana: D_5=Me . Pero también, coincide con el segundo cuartil: D_5=Q_2Me .

Cálculo de los deciles

En primer lugar buscamos la clase donde se encuentra $\displaystyle {\frac{k\cdot N}{10}, \quad k=1,2,...,9}$ , en la tabla de las frecuencias acumuladas.

\displaystyle {D_k = L_i + \frac{\frac{k\cdot N}{10} - F_{i-1}}{f_i}\cdot a_i \qquad k=1,2,...,9}

L_i es el límite inferior de la clase donde se encuentra el decil i-ésimo.

es la suma de las frecuencias absolutas.

es la frecuencia acumulada anterior a la clase el decil i-ésimo.

a_i es la amplitud de la clase o longitud del intervalo correspondiente a la clase del decil i-ésimo.

Ejercicio de deciles

Calcular los deciles de la distribución de la tabla.

Solución:

En primer lugar crearemos una nueva columna con los valores de la frecuencia acumulada. Para obtener la frecuencia acumulada realizamos lo que se indica:

Cálculo del primer decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{1\cdot 65}{10}= 6.5}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 6.5 .

La clase de D_i es: [50, 60)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_k = L_i + \frac{\frac{k\cdot N}{10} - F_{i-1}}{f_i}\cdot a_i }

\displaystyle {D_1 = 50 + \frac{6.5-0}{8}\cdot 10 = 58.12}

Cálculo del segundo decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{2\cdot 65}{10}= 13}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a .

La clase de D_2 es: [60, 70)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_2 = 60 + \frac{13-8}{10}\cdot 10 = 65 }

Cálculo del tercer decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{3\cdot 65}{10}= 19.5}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 19.5 .

La clase de D_3 es: [70, 80)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_3 = 70 + \frac{19.5-18}{16}\cdot 10 = 70.94 }

Cálculo del cuarto decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{4\cdot 65}{10}= 26}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a .

La clase de D_4 es: [70, 80)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_4 = 70 + \frac{26-18}{16}\cdot 10 = 75 }

Cálculo del quinto decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{5\cdot 65}{10}= 32.5}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 32.5 .

La clase de D_5 es: [70, 80)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_5 = 70 + \frac{32.5-18}{16}\cdot 10 = 79.06}

Cálculo del sexto decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{6\cdot 65}{10}= 39}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a .

La clase de D_6 es: [80, 90)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_6 = 80 + \frac{39-34}{14}\cdot 10 = 83.57 }

Cálculo del séptimo decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{7\cdot 65}{10}= 45.5}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 45.5 .

La clase de D_7 es: [80, 90)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_7 = 80 + \frac{45.5-34}{14}\cdot 10 = 88.21 }

Cálculo del octavo decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{8\cdot 65}{10}= 52}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a .

La clase de D_8 es: [90, 100)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_8 = 90 + \frac{52-48}{10}\cdot 10 = 94}

Cálculo del noveno decil

Buscamos la clase donde se encuentra el primer decil:

\displaystyle {\frac{k\cdot N}{10} = \frac{9\cdot 65}{10}= 58.5}

Buscamos en la columna de las frecuencias acumuladas (F_i) el intervalo que contiene a 58.5 .

La clase de D_9 es: [100, 110)

Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

\displaystyle {D_9 = 100 + \frac{58.5-58}{5}\cdot 10 =101 }

Los percentiles

Definición de percentiles

Los percentiles son los valores que dividen una serie de datos ordenados en 100 partes iguales.

Los percentiles dan los valores correspondientes al $1\%$ , al $2\%$ … y al $99\%$
de los datos.

$\textup{P}_{50}$ coincide con la mediana

$\textup{P}_{50}$ coincide con $\textup{Q}_{2}$

$\textup{P}_{50}$ coincide con $\textup{D}_{5}$

\textup{P}_{50}=\textup{Me}=\textup{Q}_{2}=\textup{D}_{5}

Cálculo de los percentiles

En primer lugar buscamos la clase donde se encuentra $\cfrac{k\cdot N}{100},\; \; \; k=1,2,...,99$ , en la tabla de las frecuencias acumuladas.

\textup{P}_{k}=L_{i}+\cfrac{\cfrac{k\cdot N}{100}-F_{i-1}}{f_{i}}\cdot a_{i}

$L_{i}$ es el límite inferior de la clase donde se encuentra el percentil

es la suma de las frecuencias absolutas

$F_{i-1}$ es la frecuencia acumulada anterior a la clase del percentil

$a_{i}$ es la amplitud de la clase

Ejercicio de percentiles

1 Calcular el percentil y de la distribución de la tabla:

\begin{matrix}\hline \textup{Intervalo} & f_{i} \\ \hline [50,60) & 8\\ [60,70) & 10\\ [70,80) & 16\\ [80,90) & 14\\ [90,100) & 10\\ [100,110) & 5\\ [110,120) & 2\\ \hline \end{matrix}

En primer lugar crearemos una nueva columna con los valores de la frecuencia acumulada:

En la primera casilla colocamos la primera frecuencia absoluta.

En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a N (65)

\begin{matrix}\hline \textup{Intervalo} & f_{i} & F_{i}\\ \hline [50,60) & 8 & 8\\ [60,70) & 10 & 18\\ [70,80) & 16 & 34\\ [80,90) & 14 & 48\\ [90,100) & 10 & 58\\ [100,110) & 5 & 63\\ [110,120) & 2 & 65\\ \hline \sum & 65 & &\\ \hline \end{matrix}

Cálculo del percentil 35

Buscamos el intervalo donde se encuentra el percentil , multiplicando por N(65) y dividiendo por 100

Buscamos en la columna de las frecuencias acumuladas $(\textup{F}_{i})$ el intervalo que contiene a 22,75

La clase de $\textup{P}_{35}$ es: [70, 80)

Aplicaremos la fórmula para el cálculo de percentiles para datos agrupados, extrayendo los siguientes datos:

\textup{P}_{35}=70+\cfrac{22,75-18}{16}\cdot 10=72,97

Cálculo del percentil 60

Buscamos el intervalo donde se encuentra el percentil , multiplicando por N(65) y dividiendo por 100

Buscamos en la columna de las frecuencias acumuladas $(\textup{F}_{i})$ el intervalo que contiene a

La clase de $\textup{P}_{60}$ es: [80, 90)

Aplicaremos la fórmula para el cálculo de percentiles para datos agrupados, extrayendo los siguientes datos:

\textup{P}_{60}=80+\cfrac{39-34}{14}\cdot 10=83,57

Desviación media

La desviación absoluta promedio o desviación media o también conocida como promedio de un conjunto de datos se puede definir como la media de las desviaciones absolutas

Desviación respecto a la media

La desviación respecto a la media es la diferencia en valor absoluto entre cada valor de la variable estadística y la media aritmética.

Desviación media

La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media y se representa por $D_{\bar{x}} \right |$

\displaystyle =\frac{\left | x_1-\bar{x} \right |+\left | x_2-\bar{x} \right |+...+\left | x_n-\bar{x} \right |}{N}

\displaystyle =\frac{\sum_{i=1}^{n}\left | x_i-\bar{x} \right |}{N}

Ejemplo:

Calcular la desviación media de la distribución:

Calculamos la media aritmética para poder hallar las desviaciones respecto a la media

\displaystyle \bar{x}=\frac{9+3+8+8+9+8+9+18}{8}=9

Aplicamos la fórmula de la desviación media

\displaystyle =\frac{\left | 9-9\right |+\left | 3-9 \right |+\left | 8-9 \right |+\left | 8-9 \right |+\left | 9-9 \right |+\left | 8-9 \right |+\left | 9-9 \right |+\left | 18-9 \right |}{8}= 2.25

Desviación media para datos agrupados

Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:

\displaystyle =\frac{\left | x_1-\bar{x} \right |f_1+\left | x_2-\bar{x} \right |f_2+...+\left | x_n-\bar{x} \right |f_n}{N}

\displaystyle =\frac{\sum_{i=1}^{n}\left | x_i-\bar{x} \right |f_i}{N}

Ejemplo de calculo de desviación media para datos agrupados

Calcular la desviación media de la distribución:

En primer lugar calculamos la media aritmética:

Incorporamos otra columna con los productos de las marcas de clase por sus frecuencias absolutas correspondientes y hacemos la suma (457.5)

Por otro lado realizamos la suma de las frecuencias absolutas (21)

\displaystyle \bar{x}=\frac{457.5}{21}=21.786

Añadimos otra columna a la tabla con las desviaciones respecto a la media $\left ( \left | x-\bar{x} \right | \right )$

Agregamos otra columna con los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes $\left ( \left | x-\bar{x} \right | \right \cdot f_i)$ y hacemos la suma (98.75)

Calculamos la desviación media

Varianza

La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.

La varianza se representa por $\displaystyle \sigma ^{2}$ .

La fórmula de la varianza

\displaystyle \sigma ^{2}=\frac{(x_1-\bar{x})^{2}+(x_2-\bar{x})^{2}+...+(x_n-\bar{x})^{2}}{N}

\displaystyle \sigma ^{2}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^{2}}{N}

Ejemplos de cálculo de la varianza

1º Calcular la varianza de la distribución: 9, 3, 8, 8, 9, 8, 9, 18.

Calculamos la media aritmética

Calculamos la varianza

\displaystyle \sigma ^{2}=\frac{(9-9)^{2}+(3-9)^{2}+(8-9)^{2}}{8}+

\displaystyle + \frac{(8-9)^{2}+(9-9)^{2}+(8-9)^{2}}{8}+

\displaystyle + \frac{(9-9)^{2}+(18-9)^{2}}{8}=15

2º Calcular la varianza de la distribución: 12, 6, 7, 3, 15, 10, 18, 5.

Calculamos la media aritmética

\displaystyle \bar{x}=\frac{12+6+7+3+15+10+18+5}{8}=\frac{76}{8}=9.5

Calculamos la varianza

\displaystyle \sigma ^{2}=\frac{(12-9.5)^{2}+(6-9.5)^{2}+(7-9.5)^{2}}{8} +

\displaystyle + \frac{(3-9.5)^{2}+(15-9.5)^{2}+(10-9.5)^{2}}{8}+

\displaystyle + \frac{(18-9.5)^{2}+(18-9.5)^{2}+(5-9.5)^{2}}{8}=23.75

3º Calcular la varianza de la distribución: 5, 5, 12, 13, 15, 15, 15, 20, 20, 23.

Usando las mismas etapas como en los ejemplos anteriores, primero calculamos la media aritmética y luego la varianza.

\displaystyle \bar{x}=\frac{5+5+12+13+15+15+15+20+20+23}{10}=\frac{143}{10}=14.3

\displaystyle \sigma ^{2}=\frac{(5-14.3)^{2}+(5-14.3)^{2}+(12-14.3)^{2}}{10}+

\displaystyle + \frac{(13-14.3)^{2}+(15-14.3)^{2}+(15-14.3)^{2}}{10}+

\displaystyle + \frac{(13-14.3)^{2}+(20-14.3)^{2}+(20-14.3)^{2}}{10}+

\displaystyle + \frac{(23-14.3)^{2}}{10}=

\displaystyle =\frac{86.49+86.49+5.29+1.69+0.49+0.49}{10}+

\displaystyle =\frac{0.49+32.49+32.49+75.69}{10}=\frac{322.1}{10}=32.21

4º Calcular la varianza de la distribución: 150, 160, 164, 158, 183.

Usando las mismas etapas como en los ejemplos anteriores, primero calculamos la media aritmética y luego la varianza.

\displaystyle \bar{x}=\frac{150+160+164+158+183}{5}=\frac{815}{5}=163

\displaystyle \sigma ^{2}=\frac{(150-163)^{2}+(160-163)^{2}+(164-163)^{2}}{5}+

\displaystyle + \frac{(158-163)^{2}+(183-163)^{2}}{5}=

\displaystyle + \frac{169+9+1+25+400}{5}=\frac{604}{5}=120.8

5º Calcular la varianza de la distribución: 2, 3, 2, 3, 1, 2, 2, 3, 1, 1, 4.

Usando las mismas etapas como en los ejemplos anteriores, primero calculamos la media aritmética y luego la varianza.

\displaystyle \bar{x}=\frac{2+3+2+3+1+2+2+3+1+1+4}{5}=\frac{22}{11}=2

\displaystyle \sigma ^{2}=\frac{(2-2)^{2}+(3-2)^{2}+(2-2)^{2}+(3-2)^{2}}{11}+

\displaystyle \sigma ^{2}=\frac{(1-2)^{2}+(2-2)^{2}+(2-2)^{2}+(3-2)^{2}+(1-2)^{2}}{11}+

\displaystyle \sigma ^{2}=\frac{(1-2)^{2}+(4-2)^{2}}{11}=

\displaystyle \frac{0+1+0+1+1+0+0+1+1+1+4}{11}=\frac{10}{11}=0.91

Varianza para datos agrupados

\displaystyle \sigma ^{2}=\frac{(x_1-\bar{x})^{2}f_1+(x_2-\bar{x})^{2}f_2+...+(x_n-\bar{x})^{2}f_n}{N}

\displaystyle \sigma ^{2}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^{2}f_i}{N}

Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

\displaystyle \sigma ^{2}=\frac{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}}{N} - \bar{x}^{2}

\displaystyle \sigma ^{2}=\sum_{i=1}^{n}\frac{x_{i}^{2}}{N} - \bar{x}^{2}

Ejemplo de cálculo de datos agrupados

Calcular la varianza de la distribución de la tabla:

Hemos añadido la columna $x_i \cdot f_i$ porque queremos hallar su sumatoria (1820) , que
después dividiremos por N (42) para obtener la media

\displaystyle \bar{x}=\frac{1820}{42}=43.33

Hemos añadido la columna $x_i \cdot f_i$ porque queremos hallar su sumatoria (88050) , que después dividiremos por N (42) y al resultado le restaremos la media aritmética al cuadrado $(43.33^{2})$

\displaystyle \sigma ^{2}= \frac{88050}{42} - 43.33^{2}= 218.94

Propiedades de la varianza

1º La varianza será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.

2º Si a todos los valores de la variable se les suma un número la varianza no varía.

3º Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por el cuadrado de dicho número.

4º Si tenemos varias distribuciones con la misma media y conocemos sus respectivas varianzas se puede calcular la varianza total.

Si todas las muestras tienen el mismo tamaño:

\displaystyle \sigma ^{2}= \frac{\sigma _{1}^{2}+\sigma _{2}^{2}+...+\sigma _{n}^{2}}{n}

Si las muestras tienen distinto tamaño:

\displaystyle \sigma ^{2}= \frac{k_{1} \cdot \sigma _{1}^{2}+k_{2} \cdot\sigma _{2}^{2}+...+k_{n} \cdot\sigma _{n}^{2}}{k_{1}+k_{2}+...+k_{n}}

Observaciones sobre la varianza

1º La varianza, al igual que la media, es un índice muy sensible a las puntuaciones extremas.

2º En los casos que no se pueda hallar la media tampoco será posible hallar la varianza.

3º La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado.

La desviación típica

La desviación típica es la raíz cuadrada de la varianza.

Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.

La desviación típica se representa por $\sigma$ .

\sigma =\sqrt{\cfrac{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}}{N}}

\sigma =\sqrt{\cfrac{\displaystyle\sum_{1=1}^{n}(x_{i}-\bar{x})^{2}}{N}}

Ejemplo

Calcular la desviación típica de la distribución:

Calculamos la media aritmética

Sustituimos en la fórmula de la desviación típica $\sigma =\sqrt{\cfrac{(9-9)^{2}+(3-9)^{2}+(8-9)^{2}+(8-9)^{2}+(9-9)^{2}+(8-9)^{2}+(9-9)^{2}+(18-9)^{2}}{8}}$
$\sigma =3,87$

Desviación típica para datos agrupados

\sigma =\sqrt{\cfrac{(x_{1}-\bar{x})^{2}\cdot f_{1}+(x_{2}-\bar{x})^{2}\cdot f_{2}+...+(x_{n}-\bar{x})^{2}\cdot f_{n}}{N}}

\sigma =\sqrt{\cfrac{\displaystyle\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}\cdot f_{i}}{N}}

Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

\sigma =\sqrt{\cfrac{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}}{N}-\bar{x}^{2}}

\sigma =\sqrt{\displaystyle\sum_{i=1}^{n}\cfrac{x_{i}^{2}}{N}-\bar{x}^{2} }

\sigma =\sqrt{\cfrac{x_{1}^{2}\cdot f_{1}+x_{2}^{2}\cdot f_{2}+...+x_{n}^{2}\cdot f_{n}}{N}-\bar{x}^{2}}

\sigma =\sqrt{\displaystyle\sum_{i=1}^{n}\cfrac{x_{i}^{2}\cdot f_{i}}{N}-\bar{x}^{2} }

Ejemplo

Calcular la desviación típica de la distribución de la tabla:

Hemos añadido la columna $x_{i}\cdot f_{i}$ porque queremos hallar su sumatoria (1.820) , que después dividiremos por $N\; (42)$ para obtener la media

Hemos añadido la columna $x_{i}^{2}\cdot f_{i}$ porque queremos hallar su sumatoria (88.050) , que después dividiremos por $N\; (42)$ y al resultado le restaremos la media aritmética al cuadrado $(43,33^{2})$ , y por último haremos la raíz cuadrada del resultado obtenido

\sigma =\sqrt{\cfrac{88.050}{42}-43,33^{2}}=14,797

Propiedades de la desviación típica

1º La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.

2º Si a todos los valores de la variable se les suma un número la desviación típica no varía.

3º Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.

4º Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.

Si todas las muestras tienen el mismo tamaño:

\sigma =\sqrt{\cfrac{\sigma_{1}^{2}+\sigma_{2}^{2}+...+\sigma_{n}^{2}}{n}}

Si las muestras tienen distinto tamaño:

\sigma =\sqrt{\cfrac{k_{1}\cdot \sigma_{1}^{2}+k_{2}\cdot\sigma_{2}^{2}+...+k_{n}\cdot\sigma_{n}^{2}}{k_{1}+k_{2}+...+k_{n}}}

Observaciones sobre la desviación típica

1º La desviación típica, al igual que la media y la varianza, es un índice muy sensible a las puntuaciones extremas.

2º En los casos que no se pueda hallar la media tampoco será posible hallar la desviación típica.

3º Cuanta más pequeña sea la desviación típica mayor será la concentración de datos alrededor de la media.

Coeficiente de variación y puntuaciones típicas

Coeficiente de variación

El coeficiente de variación es la relación entre la desviación típica de una muestra y su media.

El coeficiente de variación se suele expresar en porcentajes:

\textup{C.V.}=\cfrac{\sigma }{\bar{X}}\cdot 100

El coeficiente de variación permite comparar las dispersiones de dos distribuciones distintas, siempre que sus medias sean positivas.

Se calcula para cada una de las distribuciones y los valores que se obtienen se comparan entre sí.

La mayor dispersión corresponderá al valor del coeficiente de variación mayor.

Ejemplo:

Una distribución tiene $\bar{X}=140$ y $\sigma =28,28$ y otra $\bar{X}=150$ y $\sigma =24$ . ¿Cuál de las dos presenta mayor dispersión?

\textup{CV}_{1}=\cfrac{28,28}{140}\cdot 100=20,2 \%

\textup{CV}_{2}=\cfrac{24}{150}\cdot 100=16 \%

La primera distribución presenta mayor dispersión.

Puntuaciones típicas

Puntuaciones diferenciales

Las puntuaciones diferenciales resultan de restarles a las puntuaciones directas la media aritmética.

Puntuaciones típicas

Las puntuaciones típicas son el resultado de dividir las puntuaciones diferenciales entre la desviación típica. Este proceso se llama tipificación.

Las puntuaciones típicas se representan por .

Observaciones sobre puntuaciones típicas

La media aritmética de las puntuaciones típicas es

La desviación típica de las puntuaciones típicas es

Las puntuaciones típicas son adimensionales, es decir, son independientes de las unidades utilizadas

Las puntuaciones típicas se utilizan para comparar las puntuaciones obtenidas en distintas distribuciones

Ejemplo:

En una clase hay alumnos y alumnas. El peso medio de los alumnos es 58,2 kg y el de las alumnas 52,4 kg. Las desviaciones típicas de los dos grupos son, respectivamente, 3,1 kg y 5,1 kg. El peso de José es de kg y el de Ana es kg. ¿Cuál de ellos puede, dentro del grupo de alumnos de su sexo, considerarse más grueso?

José es más grueso respecto de su grupo que Ana respecto al suyo.

	Recuento
	I
	II



	III
	III
	I

	Alumnos	Ángulo
Baloncesto
Natación
Fútbol
Sin deporte
Total

Edad	Personas ()	Frecuencia Acumulada ()










Total:

Edad	Personas ()	Frecuencia Acumulada ()










Total:

Edad		Personas ()	Frecuencia relativa ( $f_i^{*}$ )	relativa.
				$\frac{0.09}{10} = 0.009$
				$\frac{0.13}{10} = 0.013$
				$\frac{0.19}{10} = 0.019$
				$\frac{0.38}{30} = 0.012667$
				$\frac{0.07}{10} = 0.007$
				$\frac{0.06}{10} = 0.006$
				$\frac{0.05}{10} = 0.005$
				$\frac{0.03}{10} = 0.003$
Total:

	$f_{i}$	$F_{i}$






$[72, \infty )$