CONTINUIDAD

Continuidad de una función en un punto

Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.representacoion grafica funcion continua

Se dice que una función f(x) es continua en un punto x = a si se cumplen las siguientes tres condiciones:

1 Que el punto  tenga imagen.

\exists f(a)

Es decir, debemos verificar que la función esté definida en el punto x = a. En otras palabras, que x = a pertenezca al dominio de f(x).

2 Que exista el límite de la función en el punto .

\displaystyle \exists \lim_{x\rightarrow a} f(x) \ \ \ \Leftrightarrow \ \ \ \lim_{x\rightarrow a^-} f(x) =\lim_{x\rightarrow a^+} f(x)

Si has estudiado límites, sabrás que el límite en el punto x = a existe si tiene límites por la derecha y por la izquierda y estos valores son iguales.

3 Que la imagen del punto  coincida con el límite de la función en el punto.

\displaystyle f(a)=\lim_{x\rightarrow a} f(x)

Por último, es necesario que el valor de la imagen sea igual que el valor del límite.

Ejemplos

1 Estudiar la continuidad de  en x = 2

Solución

1 Imagen en 

f(2)=4

Por lo tanto la función sí tiene imagen en el punto x=2

2 Límite en 

\displaystyle \text{Limite por la izquierda} \hspace{1cm} \longrightarrow \hspace{1cm} \lim_{x\rightarrow 2^-}x^2= 2^2 =4
\displaystyle \text{Limite por la derecha} \hspace{1cm} \longrightarrow \hspace{1cm} \lim_{x\rightarrow 2^+}4= 4

Como el límite por la derecha y el límite por la izquierda existen y son iguales, entonces

\displaystyle \lim_{x\rightarrow 2}f(x) = 4

La función sí tiene límite en el punto x = 2

3 Valor de la imagen y el límite

\displaystyle f(2)= \lim_{x\rightarrow 2}f(x) \hspace{1cm} 4=4

Sí se cumple que el valor de la imagen y el valor del límite son iguales

Concluímos que  es continua en 

En la gráfica podemos comprobarlo

representacion grafica de funciones continuas

2 Estudiar la continuidad de f(x)= \cos^{-1} x  en x = 4

Solución

1 Imagen en 

La función \cos^{-1} x  está definida solo para valores entre -1 y 1, por lo que no existe la imagen en el punto x=4 y carece de sentido hablar de continuidad en ese punto.dominio de una funcion continua representacion grafica cos - 1

La conclusión es que  no es continua en . x = 4

3 Estudiar la continuidad de en x = 2

Solución

1 Imagen en 

f(2)=2.5

Por lo tanto la función sí tiene imagen en el punto x = 2

2 Límite en 

\displaystyle \text{Limite por la izquierda} \hspace{1cm} \longrightarrow \hspace{1cm} \lim_{x\rightarrow 2^-}x= 2
\displaystyle \text{Limite por la derecha} \hspace{1cm} \longrightarrow \hspace{1cm} \lim_{x\rightarrow 2^+}2= 2

Como el límite por la derecha y el límite por la izquierda existen y son iguales, entonces

\displaystyle \lim_{x\rightarrow 2}f(x) = 2

La función sí tiene límite en el punto x = 2

3 Valor de la imagen y el límite

Tenemos que \displaystyle \lim _{x\rightarrow 2}f(x)= 2

Pero f(2)=2.5

Por lo que no se cumple que \displaystyle f(2)=\lim_{x\rightarrow 2} f(x) pues 2.5\not = 2

Concluímos que  no es continua en 

En la gráfica podemos comprobarlo

funcion no continua representacion grafica

Continuidad por la izquierda

Una función f(x) es continua por la izquierda en el punto x = a si:

Continuidad por la derecha

Una función f(x) es continua por la derecha en el punto x = a si:

Función continua

Una función f es continua en un punto si es continua por la izquierda y es continua por la derecha:

Las funciones polinómicas, racionales, con radicales, exponenciales, logarítmicas y trigonométricas son continuas en todos los puntos de su dominio.

La función 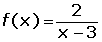 es continua en ℛ − {3}.

En x = 3 no es continua porque no está definida porque anula el denominador.

Funciones definidas a trozos

Las funciones definidas a trozos son continuas si cada función lo es en su intervalo de definición, y si lo son en los puntos de división de los intervalos, por tanto tienen que coincidir sus límites laterales.

Vamos a estudiar la continuidad de la función:

Estudiamos la continuidad en x = 1

Estudiamos la continuidad en x = 3

Estudiamos la continuidad en x = 6

La función es continua en toda ℛ.

Operaciones con funciones continuas

Si f y g son continuas en x = a, entonces:

f + g es continua en x = a.

f · g es continua en x = a.

f/g es continua en x = a, si g(a) ≠ 0.

f ο g es continua en x = a.

Si alguna de las tres condiciones continuidad de no se cumple, la función es discontinua en un punto.

condiciones de continuidad de la funcion
continuidad punto 2

La función es discontinua porque en x = 2 no existe

ejemplo funcion discontinua
condicion de la funcion
funcion
limite funcion
limite funcion

La función es discontinua porque en x = 2 no tiene límite, ya que no coinciden los límites laterales

funcion discontinua
condiciones de la funcion
funcion
limite funcion
limite funcion
funcion no coincide con el limite

La función es discontinua porque en x = 2 no coincide la imagen con el límite

funcion no es igual al limite

Discontinuidad evitable

La función {f(x)} tiene una discontinuidad evitable en {x=a} si el límite cuando {x} se aproxima a {a} existe y además se cumple alguna de las dos siguientes condiciones:

1 No existe imagen.

2 La imagen no coincide con el límite.

Discontinuidad inevitable

La función {f(x)} tiene una discontinuidad inevitable en {x=a} si se cumple alguna de las dos siguientes condiciones:

1 Los límites laterales cuando {x} se aproxima a {a} son distintos.

2 Los límites laterales cuando {x} se aproxima a {a} son {\infty} o {-\infty}.

Una discontinuidad es evitable en un punto {x = a} si existe {\displaystyle\lim_{x \to a}f(x)} y este es finito.

Nos encontramos con dos tipos de discontinuidad evitable:

Caso 1: La función no está definida en x = a

Esto significa que no existe {f(a)}

Ejemplo:

La función no está definida en {x=2}

Calculamos el límite cuando {x \to 2}

{\displaystyle\lim_{x\to 2^{+}}f(x)=4, \ \ \ \ \ \displaystyle\lim_{x\to 2^{-}}f(x)=4}

La función presenta una discontinuidad evitable en {x=2} porque tiene límite, pero no tiene imagen.

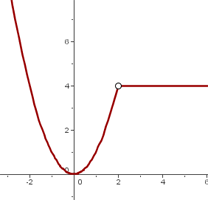
grafica de una funcion con discontinuidad evitable

Caso 2: La imagen no coincide con el límite

Esto significa que {f(a) \neq \displaystyle\lim_{x\to a}f(x)}

Ejemplo:

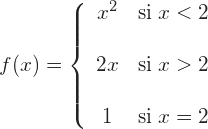
La función si está definida en {x=2}, esto es, {f(2)=1}

Calculamos el límite cuando {x \to 2}

{\displaystyle\lim_{x\to 2^{+}}f(x)=4, \ \ \ \ \ \displaystyle\lim_{x\to 2^{-}}f(x)=4}

Tenemos que {f(2) \neq \displaystyle\lim_{x\to 2}f(x)}

La función presenta una discontinuidad evitable en {x=2} porque la imagen no coincide con el límite.

representacion gráfica de funcion con discontinuidad evitable en x=2

Redefinir la función

Cuando una función presenta una discontinuidad evitable en un punto se puede redefinir en dicho punto para convertirla en una función continua.

Ejemplo:

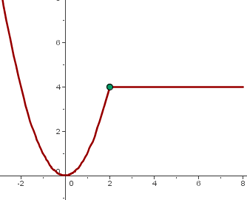
La función del caso 1 no era continua porque no tenía imagen en {x=2}

Si redefinimos la función del caso 1 conseguimos una función continua.

{f(2) = \displaystyle\lim_{x\to 2}f(x)}
grafica de funcion de discontinuidad evitable redefinida

Una discontinuidad es inevitable o de primera especie si existen los límites laterales en x = a, pero son distintos.

Salto

Salto es la diferencia en valor absoluto de los límites laterales.

Según el tipo de salto nos encontramos con dos tipos de discontinuidad inevitable:

1. Discontinuidad inevitable de salto finito

La diferencia entre los límites laterales es un número real.

Ejemplo

Salto = |4 – 1| = 3

En x = 2 hay una discontinuidad inevitable de salto finito 3

2. Discontinuidad inevitable de salto infinito

La diferencia entre los límites laterales es infinito.

Ejemplo

En x = 2 hay una discontinuidad inevitable de salto infinito

Una discontinuidad es esencial o de segunda especie si no existe alguno de los límites laterales en x = a.

Ejemplos

1. 

En x = 2 hay una discontinuidad esencial porque no tiene límite por la derecha.

2. 

En x = 2 hay una discontinuidad esencial porque no tiene límite por la izquierda.