ECUACIONES DE LA RECTA

ECUACIÓN VECTORIAL DE LA RECTA

ECUACIONES PARAMÉTRICAS DE LA RECTA

ECUACIÓN CONTINUA DE LA RECTA

PENDIENTE

1 Pendiente dado el ángulo

2 Pendiente dado el vector director de la recta

3 Pendiente dados dos puntos

ECUACIÓN GENERAL DE LA RECTA

ECUACIÓN EXPLÍCITA DE LA RECTA

ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS

ECUACIÓN CANÓNICA O SEGMENTARIA

RECTAS EN EL EJE DE COORDENADAS

RECTAS PARALELAS AL EJE OX

RECTAS PARALELAS AL EJE OY

RECTAS PARALELAS

Dos rectas son paralelas si tienen el mismo vector director o la misma pendiente.

POSICIONES RELATIVAS A DOS RECTAS

POSICIONES RELATIVAS DE DOS RECTAS

1 Si , las rectas son secantes, se cortan en un punto.

2 Si , las rectas paralelas, no se cortan en ningún punto.

3 Si , las rectas son coincidentes, todos sus puntos son comunes.

Ecuación vectorial de la recta

representación gráfica de la ecuación de la recta vectorial

¿QUE ES UNA RECTA?

Una de las primeras nociones aprendidas en matemáticas es que una recta es en realidad un conjunto de puntos sin curva o ángulos, y que estos puntos tengan la misma dirección.

¿QUE ES LA ECUACIÓN VECTORIAL DE LA RECTA?

La dirección de los puntos, está dada por un vector $\vec v$ .

Para entender la ecuación vectorial de la recta, definimos una recta como un conjunto de puntos del plano, alineados con un punto y con una dirección dada $\vec v$ .

Si P(x_1,y_1) es un punto de la recta , el vector, $\overrightarrow{PX}$ o la direccion de este punto P, tiene la misma direccion que la recta y entonces también la misma dirección que $\vec v$ .

El vector $\overrightarrow{PX}$ es igual al $\vec v$ multiplicado por un escalar:

\overrightarrow{PX} = k \cdot \vec v \ \ \ \ \ \ \ \ \ \ k \in \mathbb{R}

\overrightarrow{PX} = \overrightarrow{OX} - \overrightarrow{OP} \ \ \ \ \ \ \ \ \ \ \overrightarrow{PX} - \overrightarrow{OP} = k \cdot \vec v

\vec OX = \overrightarrow{OP} + k \cdot \vec v

EJEMPLO DE ECUACIÓN VECTORIAL

Una recta pasa por el punto A(-1,3) y tiene un vector director $\vec v = (2,5)$ . Escribir su ecuación vectorial.

La ecuación paramétrica de la recta

Seguramente ya estás familiarizado con la ecuación de una recta de la forma:

Donde:

: es la pendiente o inclinación de la recta

: es el cruce con el eje ”

Pero, una recta puede representarse también mediante un sistema de ecuaciones de la siguiente manera:

\left\{\begin{matrix} x=a_{1}+\lambda v_{1}\\y=a_{2}+\lambda v_{2} \end{matrix}\right.

Cada ecuación contiene los valores de todos los puntos de la recta para e , respectivamente.

$a_{1}$ y $a_{2}$ son las coordenadas del punto conocido $A\left ( a_{1},a_{2} \right )$ por el cual pasa la recta.
$v_{1}$ y $v_{2}$ son las coordenadas de un vector director, $\vec{v}=\left ( v_{1},v_{2} \right )$ , que nos indica la dirección de la recta
$\lambda$ es un número real que nos permitirá conocer cualquier coordenada de la recta según el valor que se le asigne.

Observa la siguiente figura:

representacion grafica ecuacion de la recta

Como puedes observar, la recta ‘‘ pasa por el punto $A\left ( 1,4 \right )$ y las coordenadas del vector director son $\vec{v}\left ( 1,2 \right )$ El vector director siempre será paralelo a la recta ‘‘La ecuación de la recta ‘‘ puede escribirse como:

\left\{\begin{matrix} x=1+\lambda \\y=4+2\lambda \end{matrix}\right.

EJEMPLO DE PROBLEMA CON LA ECUACIÓN PARAMÉTRICA

Una recta pasa por el punto A(-1,3) y tiene un vector director $\vec{v}=(2,5)$ . Escribir sus ecuaciones paramétricas.

ejemplo de representacion grafica de la ecuacion de la recta y su vector director

Sabemos que $a_{1}=-1$ y $a_{2}=3$
además $v_{1}=2$ y $v_{2}=5$

por lo que:

\left\{\begin{matrix} x=-1+2\lambda \\y=3+5\lambda \end{matrix}\right.

Y su gráfica sería:

Ecuación continua de la recta

Si de las ecuaciones paramétricas despejamos el parámetro k.

Y si igualamos, queda:

Ejemplo:

Una recta pasa por el punto A(-1, 3) y tiene un vector director = (2,5). Escribir su ecuación continua.

La ecuación general de la recta

ECUACIÓN CONTINUA HACIA LA ECUACIÓN GENERAL DE RECTA

1 Tomamos la ecuación continua la recta

\frac{x-x_{1}}{v_{1}} = \frac{y-y_{2}}{v_{2}}

2 Despejamos los denominadores y obtenemos:

v_{2}x - v_{2}x_{1} = v_{1}y - v_{1}y_{1}

3 Trasponemos los términos.

4 Usamos A, B, y C para simplificar.

{\ A=v_2, \ \ \ B=-v_1, \ \ \ C=v_1y_1-v_2x_1}

Así es como obtenemos la siguiente ecuación, la ecuación de la recta.

LA ECUACIÓN GENERAL DE LA RECTA

Esta expresión recibe el nombre de ecuación general o implícita de la recta.

LAS COMPONENTES DEL VECTOR DIRECTOR

LA PENDIENTE DE LA RECTA

ECUACIÓN CON PUNTO A Y PENDIENTE M HACIA LA ECUACIÓN GENERAL DE RECTA

Como podrás notar no es complicado obtener la ecuación general de la recta, para ello basta considerar cualquier representación de la misma y despejar los elementos de manera que se obtenga una ecuación igual a cero.

Para el caso de la ecuación general de la recta a partir de la de la ecuación de la recta con punto A=(x_1,y_1) y pendiente , tenemos: ${\ y-y_1=m(x-x_1)}$ . Los pasos para llegar a la ecuación general de la recta son los siguientes:

1 Desarrollamos la multiplicación del lado derecho de la igualdad

2 Despejamos la ecuación e igualamos a cero

3 Usamos A, B, y C para simplificar.

4 Y obtenemos otra vez la ecuación general de la recta:

EJEMPLOS DE EJERCICIOS DE ECUACIÓN DE LA RECTA

1 Hallar la ecuación de la que pasa por el punto A(1,5) y tiene como vector director $\vec v = (-2,1)$ .

Como tenemos los valores del punto A(1,5) y del vector director $\vec v = (-2,1)$ , sustituimos estos valores en la ecuación continua de la recta.

Despejamos los denominadores y obtenemos

Igualando la ecuación a cero, obtenemos la ecuación general de la recta

2 Hallar la ecuación de la que pasa por el punto A=(1,5) y tiene pendiente m=-2

Como tenemos los valores del punto y de la pendiente , sustituimos estos valores en la ecuación punto pendiente de la recta

Desarrollamos la multiplicación

Igualamos a cero y obtenemos la ecuación general de la recta

Ecuación explícita de la recta

Si en la ecuación general de la recta

despejamos y, se obtienen:

El coeficiente de la x es la pendiente, m.

El término independiente, b, se llama ordenada en el origen de una recta siendo (O, b) el punto de corte con el eje OY.Ejemplo:

Hallar la ecuación en forma explícita de la recta que pasa por A (1,5) y tiene como pendiente m=-2.

La ecuación punto-pendiente de la recta

PENDIENTE DE UNA RECTA

Considera la recta de la siguiente figura. La pendiente de la recta es la tangente del ángulo $alfa$ que forma la recta con la dirección positiva del eje . En otras palabras, si $\alpha$ es el ángulo entre la recta y el eje , entonces la pendiente es $tangente de alfa$ .

La pendiente se suele denotar utilizando la . Algunas fórmulas para calcular la pendiente son las siguientes:

1 Pendiente dado el ángulo

Si ya conocemos el ángulo $alfa$ que se forma entre la recta y el eje $x$ positivo, entonces la pendiente se calcula mediante:

2 Pendiente dado el vector director de la recta

La recta se puede definir por medio de un vector-dirección $vector director$ y un punto $punto A$ (que está en la recta). Esta manera de definir una recta se conoce como ecuación paramétrica de la recta. En este caso, la pendiente se obtiene utilizando:

Observemos que la pendiente no depende del punto; únicamente depende del vector director.

3 Pendiente dados dos puntos

Recordemos que la tangente del ángulo de un triángulo rectángulo se define como $tangente en triangulo rectangulo$ , donde $cateto opuesto$ es la longitud del cateto opuesto y $cateto adyacente$ es la longitud del cateto adyacente.

De este modo, si miramos la imagen del principio, podemos ver que $valor cateto opuesto$ y $valor cateto adyacente$ . Sustituyendo, tenemos que,

\tan(\alpha) = \displaystyle \frac{\text{CO}}{\text{CA}} = \frac{y_2 - y_1}{x_2 - x_1}

Así, la pendiente de la recta que pasa por los puntos $punto A$ y $punto B$ se calcula mediante:

m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}

INTERPRETACIÓN DE LA PENDIENTE

Observemos la siguiente figura donde el ángulo $alfa$ está entre $0 grados$ y $90 grados$ —es decir, el ángulo es agudo—.

Si el ángulo que forma la recta $r$ con la parte positiva del eje $x$ es agudo, entonces la pendiente es positiva e incrementa al crecer el ángulo —siempre que el ángulo se mantenga menor a $90 grados$ —. Intuitivamente, la pendiente mide “qué tan inclinada” está la recta: una pendiente grande significa que la recta está muy inclinada hacia arriba.

Ahora observa la siguiente figura donde el ángulo $alfa$ es mayor a $90 grados$ , pero menor a $180 grados$ .

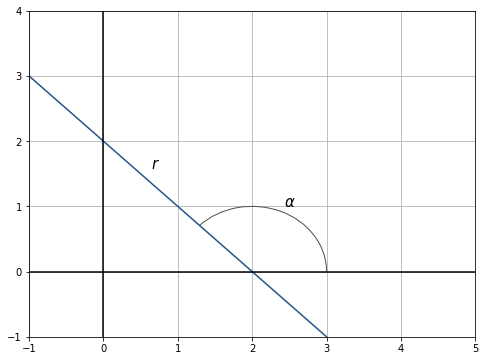
Si el ángulo que forma la recta $r$ con la parte positiva del eje $x$ es obtuso —mayor a $90 grados$ , pero menor a $180 grados$ —, la pendiente es negativa y tiende a 0 cuando crece el ángulo. Igualmente, una pendiente negativa también mide qué tan inclinada está la recta; sin embargo, en este caso una pendiente negativa muy grande indica que la recta se encuentra muy inclinada “hacia abajo”.

ECUACIÓN PUNTO-PENDIENTE DE LA RECTA

Ahora vamos a obtener la ecuación punto-pendiente de la recta. Se puede empezar desde distintas ecuaciones de la recta, nosotros empezaremos de la ecuación continua (o normal) de la recta —donde $x 1 y 1$ es un punto que está en la recta y $v$ es el vector director—,

\displaystyle \frac{x - x_1}{v_1} = \frac{y - y_1}{v_2}

Multiplicando ambos lados por $v 2$ , obtenemos,

\displaystyle y - y_1 = \frac{v_2}{v_1}(x - x_1)

Luego, como,

Entonces, se obtiene:

La cual se conoce como ecuación punto-pendiente de la recta.

Nota: Para calcular la ecuación punto-pendiente de la recta siempre necesitamos un punto $x 1 y 1$ y la pendiente $m$ (la cual se puede calcular utilizando cualquiera de las formas que describimos al principio).

EJEMPLOS

1 Tenemos una recta pasa por el punto $menos 1, 3$ y tiene un vector director $2, 5$ . Escribe su ecuación punto-pendiente.

Solución: Se nos proporcionó un vector director $v$ , por lo que su pendiente está dada por

\displaystyle m = \frac{v_2}{v_1} = \frac{5}{2}

De esta manera, sustituyendo en la ecuación punto-pendiente con $x 1 igual a menos 1$ e $y 1 igual a 3$ , tenemos que

{ \displaystyle y - 3 = \frac{5}{2}(x + 1) }

Ten cuidado con los signos, ya que $x menos menos 1 es igual a x mas 1$ .

2 Encuentra la ecuación punto-pendiente de la recta que pasa por los puntos $menos 2, menos 3$ y $4, 2$ .

Solución: En esta ocasión tenemos dos puntos que están en la recta, por lo tanto, la pendiente se calcula mediante:

\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - (-3)}{4 - (-2)} = \frac{2 + 3}{4 + 2} = \frac{5}{6}

Así, al sustituir en la ecuación punto-pendiente, se obtiene

\displaystyle y + 3 = \frac{5}{6}(x + 2) }

3 Halla la ecuación punto-pendiente de la recta que pasa por $menos 2, menos 3$ y tiene una inclinación de $45 grados$ .

Solución: Por último, se nos proporcionó el ángulo que hay entre la recta y el eje . Así, la pendiente está dada por,

De manera que la ecuación recta-pendiente es:

Es decir,

Rectas paralelas

1 Dos rectas son paralelas si sus vectores directores son paralelos, es decir, si éstos son linealmente dependientes.

\cfrac{u_{1}}{u_{2}}=\cfrac{v_{1}}{v_{2}}

2 Dos rectas son paralelas si tienen sus vectores directores iguales.

3 Dos rectas son paralelas si tienen sus pendientes iguales.

4 Dos rectas son paralelas si los coeficientes de e respectivos son proporcionales.

\cfrac{A_{1}}{B_{1}}=\cfrac{A_{2}}{B_{2}}

5 Dos rectas son paralelas si forman un ángulo de $0^{\circ}$ .

\begin{matrix} & & r\equiv Ax+By+C=0 & & & &\vec{V}_{r}=\vec{V}_{s}=(-B,A) \\ & & & & & &\\ r\parallel s & & & & & &\\ & & & & & &\\ & & s\equiv Ax+By+k=0 & & k\, \epsilon \, \mathbb{R} & &m_{r}=m_{s}=-\cfrac{A}{B}=\cfrac{v_{2}}{v_{1}} \end{matrix}

EJEMPLOS

1 Calcular una recta paralela a $r\equiv x+2y+3=0$ , que pasen por el punto A(3,5) .

2 Calcula para que las rectas $r\equiv x+2y-3=0$ y $s\equiv x-ky+4=0$ , sean paralelas.

m_{r}=-\cfrac{1}{2}\; \; \; \; \; \; \; \; \; \; m_{s}=\cfrac{1}{k}

r\parallel s\; \; \; \; \; \Rightarrow \; \; \; \; \; -\cfrac{1}{2}=\cfrac{1}{k}\; \; \; \; \; \Rightarrow \; \; \; \; \; k=-2

3 Hallar la ecuación de la recta paralela a $r\equiv 3x+2y-4=0$ , que pasa por el punto A(2,3)

3\cdot 2+2\cdot 3+k=0\; \; \; \; \; \Rightarrow \; \; \; \; \; k=-12

4 La recta $r\equiv 3x+ny-7=0$ pasa por el punto A(3,2) y es paralela a la recta $s\equiv mx+2y-13=0$ . Calcula y .

3\cdot 3+n\cdot 2-7=0\; \; \; \; \; \Rightarrow \; \; \; \; \; n=-1

\cfrac{3}{m}=\cfrac{-1}{2}\; \; \; \; \; \Rightarrow \; \; \; \; \; m=-6

Ejercicios de incidencia

RECORDATORIO

Un punto $P(p_{1},p_{2})$ pertenece a una recta de ecuación Ax+By+C=0 , cuando las coordenadas del punto satisfacen la igualdad:

Cuando un punto P pertenece a una recta r se dice que r incide en P o que r pasa por P.

EJERCICIOS PROPUESTOS

1 Determina si el punto P(-2,5) incide con la recta $r\equiv 2x+3y-11=0$

Solución

Determina si el punto P(-2,5) incide con la recta $r\equiv 2x+3y-11=0$

1 Sustituimos el punto P en la ecuación de la recta r y verificamos si se cumple la igualdad

2 Como la igualdad se cumple, el punto P incide con la recta r

2 Determina si el punto P(0,-7) incide con la recta $r\equiv 5x-2y+5=0$

Solución

Determina si el punto P(0,-7) incide con la recta $r\equiv 5x-2y+5=0$

1 Sustituimos el punto P en la ecuación de la recta r y verificamos si se cumple la igualdad

2 Como la igualdad no se cumple, el punto P no incide con la recta r

3Encuentra el punto en que las rectas $r_{1}\equiv 2x+5y-19=0$ y $r_{2}\equiv 3x-4y+6=0$ inciden

Solución

Encuentra el punto en que las rectas $r_{1}\equiv 2x+5y-19=0$ y $r_{2}\equiv 3x-4y+6=0$ inciden

1 Planteamos un sistema de ecuaciones con las rectas $r_{1}$ y $r_{2}$

\left\{\begin{matrix} 2x+5y-19=0\\ \\ 3x-4y+6=0 \end{matrix}\right.

2 Resolveremos el sistema por el método de Reducción. Para ello, multiplicamos por 4 a $r_{1}$ y por 5 a $r_{2}$

\left\{\begin{matrix} 4(2x+5y-19)=0(4)\\ \\ 5(3x-4y+6)=0(5) \end{matrix}\right.

\left\{\begin{matrix} 8x+20y-76)=0\\ \\ 15x-20y+30)=0 \end{matrix}\right.

3 Sumamos ambas ecuaciones

4 Despejamos a ‘x’

5 Sustituimos el valor de ‘x’ en cualquiera de las ecuaciones, en este caso lo sustituiremos en $r_{1}$ , y despejamos a ‘y’

Las rectas $r_{1}$ y $r_{2}$ inciden en el punto P(2,3)

4Encuentra el punto en que las rectas $r_{1}\equiv x+6y-10=0$ y $r_{2}\equiv -3x-18y+30=0$ inciden

Solución

Encuentra el punto en que las rectas $r_{1}\equiv x+6y-10=0$ y $r_{2}\equiv -3x-18y+30=0$ inciden

1 Planteamos un sistema de ecuaciones con las rectas $r_{1}$ y $r_{2}$

\left\{\begin{matrix} x+6y-10=0\\ \\ -3x-18y+30=0 \end{matrix}\right.

2 Resolveremos el sistema por el método de Reducción. Para ello, multiplicamos por 3 a $r_{1}$

\left\{\begin{matrix} 3(x+6y-10)=0(3)\\ \\ -3x-18y+30=0 \end{matrix}\right.

\left\{\begin{matrix} -3x-18y+30=0\\ \\ -3x-18y+30=0 \end{matrix}\right.

3 Sumamos ambas ecuaciones

4 Como todos los términos se cancelan significa que las rectas tienen una infinidad de puntos de incidencia. Para encontrar al menos 1 de ellos le podemos asignar un valor a una de las variables y despejar la otra, de cualquier ecuación. Por ejemplo, sustituyamos x=2 en $r_{1}$

Uno de los puntos de incidencia de las rectas $r_{1}$ y $r_{2}$ es $P\left (2,\frac{4}{3} \right )$

5Encuentra el punto en que las rectas $r_{1}\equiv 3x-2y-5=0$ y $r_{2}\equiv 3x-2y+30=0$ inciden

Solución

Encuentra el punto en que las rectas $r_{1}\equiv 3x-2y-5=0$ y $r_{2}\equiv 3x-2y+30=0$ inciden

1 Planteamos un sistema de ecuaciones con las rectas $r_{1}$ y $r_{2}$

\left\{\begin{matrix} 3x-2y-5=0\\ \\ 3x-2y+30=0 \end{matrix}\right.

2 Resolveremos el sistema por el método de Reducción. Para ello, multiplicamos por -1 a $r_{1}$

\left\{\begin{matrix} -1(3x-2y-5)=0(-1)\\ \\ 3x-2y+30=0 \end{matrix}\right.

3 Sumamos ambas ecuaciones

Como llegamos a una inconsistencia, las rectas $r_{1}$ y $r_{2}$ no tienen puntos de incidencia.

6Calcula el valor de ‘a’ para que la recta $r_{1}\equiv ax-3y-9=0$ incida con el punto P(-3,-5)

Solución

Calcula el valor de ‘a’ para que la recta $r_{1}\equiv ax-3y-9=0$ incida con el punto P(-3,-5)

1 Sustituimos el punto P(-3,-5) en $r_{1}$

2 Despejamos a ‘a’

7Calcula el valor de ‘a’ para que la recta $r_{1}\equiv ax-3y-9=0$ incida con el punto P(-3,-5)

Solución

Calcula los valores de ‘a’ y ‘b’ para que las rectas $r_{1}\equiv ax-by+7=0$ incida con la recta $r_{2}\equiv bx+ay+11=0$ en el punto P(-2,-1)

1 Sustituimos el punto P(-2,-1)
en $r_{1}$ y $r_{2}$ y planteamos un sistema de ecuaciones

\left\{\begin{matrix} ax-by+7=0\\ \\ bx+ay+11=0 \end{matrix}\right.

\left\{\begin{matrix} -2a+b+7=0\\ \\ -2b-a+11=0 \end{matrix}\right.

2 Multiplicamos por -2 la segunda ecuación

\left\{\begin{matrix} -2a+b+7=0\\ \\ (-2)(-2b-a+11)=0(-2) \end{matrix}\right.

\left\{\begin{matrix} -2a+b+7=0\\ \\ 4b+2a-22=0 \end{matrix}\right.

3 Sumamos las dos ecuaciones y despejamos a ‘b’

4 Sustituimos b=3 en la primer ecuación y despejamos a ‘a’

8 En una granja se tienen 19 animales entre gallinas y caballos. El número de patas entre las dos especies de animales es 52. ¿Cuántos animales hay de cada tipo?

Solución

En una granja se tienen 19 animales entre gallinas y caballos. El número de patas entre las dos especies de animales es 52. ¿Cuántos animales hay de cada tipo?

1 Si ‘x’ es el número de gallinas y ‘y’ el número de caballos, podemos plantear un sistema de ecuaciones:

\left\{\begin{matrix} r_{1}\equiv x+y-19=0\\ \\ r_{2}\equiv 2x+4y-52=0 \end{matrix}\right.

2 El punto de incidencia entre $r_{1}$ y $r_{2}$ corresponde a la solución del problema, por lo que resolveremos el sistema por el método de reducción, multiplicamos a $r_{1}$ por -2

\left\{\begin{matrix} -2(x+y-19)=0(-2)\\ \\ 2x+4y-52=0 \end{matrix}\right.

\left\{\begin{matrix} -2x-2y+38)=0\\ \\ 2x+4y-52=0 \end{matrix}\right.

3 Sumamos ambas ecuaciones y despejamos ‘y’

4 Sustituimos y=7 en $r_{1}$ y despejamos a ‘x’

5 Las rectas $r_{1}$ y $r_{2}$ inciden en el punto P(12,7) por lo que hay 12 gallinas y 7 caballos

9Encuentra el valor de ‘a’ para que la recta $r\equiv 5x-6y+9=0$ incida con el punto P(-3,10)

Solución

Encuentra el valor de ‘a’ para que la recta $r\equiv 5x-ay+9=0$ incida con el punto P(-3,10)

1 Sustituimos el punto P en la recta r

2 Despejamos a ‘a’

10Encuentra el valor de ‘a’ para que la recta $r\equiv ax+4y-11=0$ incida con el punto P(0,0)

Solución

Encuentra el valor de ‘a’ para que la recta $r\equiv ax+4y-11=0$ incida con el punto P(0,0)

1 Sustituimos el punto P en la recta r

2 Como llegamos a una inconsistencia, la recta ‘r’ no incide con el origen de coordenadas

11Encuentra el valor de ‘a’ para que la recta $r\equiv ax+8y-10=0$ incida con el punto P(-3,0)

Solución

Encuentra el valor de ‘a’ para que la recta $r\equiv ax+8y-10=0$ incida con el punto P(-3,0)

1 Sustituimos el punto P en la recta r y despejamos ‘a’

Ecuación segmentaria o Canónica

¿QUÉ ES LA ECUACIÓN CANÓNICA O SEGMENTARIA?

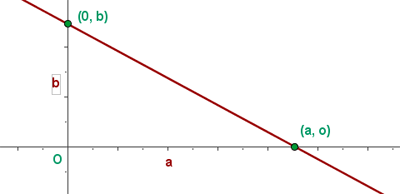
La ecuación canónica o segmentaria de la recta, es la expresión algebraica de la recta que se determina conociendo a los valores dónde la recta corta a cada uno de los ejes coordenados.

El valor donde la recta corta al eje le llamaremos , y el valor donde la recta corta al eje le llamaremos , generando los dos puntos en el plano cartesiano (a, 0) y (0, b) respectivamente.

En muchas ocasiones, tenemos la ecuación general de la recta, y partiendo de ahí necesitamos la ecuación canónica, por esta razón veamos el proceso algebraico a seguir, para que también de esta manera conozcamos la estructura de la ecuación canónica de la recta.

Comencemos con le ecuación general de la recta.

ECUACIÓN GENERAL DE LA RECTA

ECUACIÓN CANÓNICA A PARTIR DE LA ECUACIÓN GENERAL DE LA RECTA

Sabiendo que la ecuación general de la recta es:

Suponemos que x=0 con la finalidad de saber el lugar donde la recta corta al eje , entonces la ecuación general queda:

despejamos a ,

El valor encontrado corresponde a , de la ecuación canónica

y usando el mismo razonamiento podemos conocer al valor , de la ecuación canónica

RESUMEN DEL PROCESO PARA ENCONTRAR LA ECUACIÓN CANÓNICA

Si la ecuación general de la recta es:

Entonces,

y así la forma que tiene la ecuación canónica es

Ya que, si partimos de la forma general

y movemos del otro lado de la igualdad al independiente

y luego dividimos entre (el cual debe de ser distinto de cero) tenemos

\displaystyle \frac{Ax}{-C}+\frac{By}{-C}=\frac{-C}{-C}

llegamos a que

\displaystyle \frac{x}{-\frac{C}{A}}+\frac{y}{-\frac{C}{B}}=1

y entonces, así es como queda la ecuación canónica de la recta

Donde

a es la abscisa en el origen de la recta.
b es la ordenada en el origen de la recta.
El independiente de la general NO debe ser cero, significa que la forma canónica de la recta NO describe a las rectas que pasan por el origen, ya que ahí
Si o de la ecuación general son cero, significa que la recta es horizontal o vertical respectivamente, lo que lleva a que o de la ecuación canónica no existen, entonces tampoco hay forma de la ecuación canónica para este caso.

FÓRMULA DE LA ECUACIÓN CANÓNICA

EJEMPLOS DE PROBLEMAS CON LA ECUACIÓN CANÓNICA

1 Una recta determina sobre los ejes coordenados, segmentos de y unidades, respectivamente.Hallar su ecuación.

En este caso es simple, ya que de la información vemos que a=5 y b=3 , por lo que solamente es necesario sustituir los valores en la ecuación

2 Hallar la ecuación canónica de la recta que pasa por P(-2, 1) y tiene por vector director $\vec{v}=(3, -4)$ .

Observamos que por la información que nos presentan, es conveniente ocupar la ecuación de la recta en su forma continua, para esto recordemos un poco de su estructura.

Si tenemos

Un punto por donde pasa la recta
Un vector director $\vec{V}=(a, b)$ .

entonces la ecuación de la recta en su forma continua es

$\displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}$ .

Con esto, podemos hallar la ecuación en forma continua:

$\displaystyle \frac{x+2}{3}=\frac{y-1}{-4}$ .

y con esta ecuación ya podemos transformarla en la forma de la ecuación canónica.

Primero pasamos a la general, y de ahí obtenemos los valores de y :

Movemos los denominadores multiplicando al otro lado de la igualdad

movemos a las expresiones de un solo lado de la igualdad, escribiendo la forma de la ecuación general

observamos que el independiente y los valores y de la general son distintos de cero.

Entonces ya podemos calcular a la forma canónica de la recta donde $\displaystyle a=-\frac{5}{4}$ y $\displaystyle b=-\frac{5}{3}$ , llegando a que

\displaystyle \frac{x}{-\frac{5}{4}}+\frac{y}{-\frac{5}{3}}=1

Por otro lado, comentemos que la ecuación de la recta en su forma canónica nos brinda la información necesaria para poder realizar otros cálculos, por ejemplo de la recta x-y+4=0 que forma un triángulo con los ejes, podemos calcular dicha área.

Veamos, la recta forma un triángulo rectángulo con el origen y sus catetos son la abscisa y la ordenada en el origen, en otras palabras, los valores de a y b de la forma canónica

Entonces la ecuación canónica es:

\displaystyle \frac{x}{-4}+\frac{y}{4}=1

y entonces el área es:

\displaystyle A=\left |\frac{-4\cdot 4}{2} \right |=8u^{2}

ocuparemos este resultado para nuestro siguiente ejercicio.

3 Una recta pasa por el punto A(1,5) y determina con los ejes de coordenadas un triángulo de $\displaystyle 18u^{2}$ de superficie. ¿Cuál es la ecuación de la recta?

Aplicamos x=1 , y=5 a la ecuación canónica:

por otro lado el área del triángulo que genera la recta con los ejes es:

generándose así un sistema de ecuaciones (dos ecuaciones dos incógnitas)

Resolvemos el sistema:

Si en la primer ecuación multiplicamos por y en la segunda por , se forma el siguiente sistema

\displaystyle \left\{\begin{matrix} b+5a & = & ab \\ ab & = & 36 \end{matrix}\right.

Para resolverlo, multiplicamos a ambas ecuaciones por a

\displaystyle\left\{\begin{matrix} ab+5a^2 & = & a^2b \\ a^2b & = & 36a \end{matrix}\right.

luego sustituimos $\displaystyle ab=36$ , $\displaystyle a^{2}b=36a$ en la ecuación $\displaystyle ab+5a^{2}=a^{2}b$ y llegamos a la siguiente ecuación de segundo grado $\displaystyle 36+5a^{2}=36a$ , que acomodándola queda $\displaystyle 5a^{2}-36a+36=0$ .

Resolviendo a la ecuación de segundo grado, llegamos a que se tienen dos soluciones reales (hay dos rectas que cumplen la condición)

$\displaystyle a=\frac{6}{5}$ y $\displaystyle a=6$

entonces para saber el valor de , ocupamos el despeje de una igualdad, es decir $\displaystyle b=\frac{36}{a}$

$\displaystyle b=\frac{36}{a}=\frac{36}{\frac{6}{5}}=30$ y $\displaystyle b=\frac{36}{a}=\frac{36}{6}=6$

Significa que las dos ecuaciones de las rectas que cumplen la condición son

$\displaystyle\frac{x}{\frac{6}{5}}+\frac{y}{30}=1$ y $\displaystyle\frac{x}{6}+\frac{y}{6}=1$

4 Sabemos que una recta pasa por el punto A(3, 2) y que determina sobre los ejes coordenados, segmentos de doble longitud en el eje de abscisas, que en el de ordenadas. Hallar la ecuación de esta recta.