LIMITES

El límite de una función

Límite de una función en un punto

El límite de la función f(x) en el punto x_0, es el valor al que se acercan las imágenes (las f(x)=y, puntos del codominio) cuando los puntos del dominio (las x) se acercan al valor x_0. Es decir, diremos que L es el límite de f(x) cuando los puntos del dominio xtienden a f(x) es L.

A la proposición L es el límite de f(x) cuando x tiende a x_0, la denotamos así:

{ L=\lim_{x\rightarrow x_0 }f(x) }

Ejemplo de límite de una función en un punto

Vamos a estudiar el límite de la función f(x)=x^{2} en el punto x_0=2

f(x)
1,93,61
1,993,9601
1,9993,996001
......
↓↓
24
xf(x)
2,14.41
2,014,0401
2,0014,004001
......
↓↓
24

Tanto si nos acercamos a 2 por la izquierda o la derecha las imágenes se acercan a 4. Por tanto, el límite de la función en 2 es L=4.

Definición de límite de una función en un punto por épsilon y delta

Se dice que la función f(x)tiene como límite el número {L\in\mathbb{R}}, cuando xtiende a x_0, si fijado un número real positivo \varepsilon , mayor que cero, existe un numero positivo \delta dependiente de \varepsilon , tal que, para todos los valores de xdistintos de x_0 que cumplen la condición

, se cumple que

Esto es,

La idea gráfica es la siguiente:

representacion gráfica del límite de una función en x

Definición de límite de una función en un punto a través de entornos

{\lim_{x\rightarrow x_0}f(x)=L } si y sólo si, para cualquier entorno de L que tomemos, por pequeño que sea su radio  \varepsilon , existe un entorno de x_0, E_\delta (x_0), cuyos elementos (sin contar x_0), tienen sus imágenes dentro del entorno de L, E_\varepsilon(L).

Límite por la derecha y por la izquierda

Definiciones de límites de funciones

Diremos que el límite de una función \displaystyle f(x) cuando \displaystyle x  tiende hacia \displaystyle a  por la izquierda es \displaystyle L .\displaystyle \lim_{x \to a^{-}}f(x)=L

si y sólo si para todo   0 «>  existe  0 «>  tal que para todo \displaystyle x \in \left ( a-\delta, a \right )  entonces

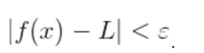
es decir

Diremos que el límite de una función \displaystyle f(x)  cuando \displaystyle x  tiende hacia \displaystyle a  por la derecha es \displaystyle L \displaystyle \lim_{x \to a^{+}}f(x)=L si y sólo si para todo   0 «>  existe  0 «>  tal que para todo \displaystyle x \in \left ( a, a+\delta \right )   entonces

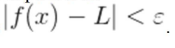
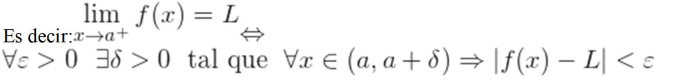
Si el límite de una función en un punto existe, este es único.

Ejemplos de funciones, limites, y gráficas

1   Sea

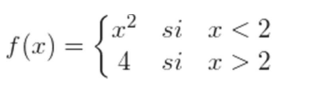
cuya gráfica es:

Ejemplo de grafica de funcion con limites laterales

Al acercarnos al circulo sobre la curva roja podemos observar que:

\displaystyle \lim_{x\to 2^{-}}f(x)=\lim_{x\to 2^{-}}x^2=4

Al acercarnos al circulo sobre la recta verde podemos observar que:

\displaystyle \lim_{x\to 2^{+}}f(x)=\lim_{x\to 2^{+}}4=4

En este caso vemos que el límite tanto por la izquierda como por la derecha cuando \displaystyle x \to 2  es \displaystyle 4.

El límite de la función es \displaystyle 4  por ser iguales los dos límites laterales, aunque la función no tenga imagen en \displaystyle x=2 . Este hecho muestra que un límite se trata de un proceso de aproximación infinitesimal, y no de sustitución directa en el valor al que se le aproxima

Desde otro punto de vista podemos decir, para calcular el límite de una función en un punto, no nos interesa lo que sucede en dicho punto sino a su alrededor.

2 Consideremos a la función definida de la siguiente manera

su gráfica es:

ejemplo de grafica de funcion

Si calculamos el límite lateral por la izquierda al cero tenemos

\displaystyle \lim_{x\to 0^{-}}f(x)=\lim_{x\to 0^{-}}(-1)=-1

y el límite lateral por la derecha al cero tenemos

\displaystyle \lim_{x\to 0^{+}}f(x)=\lim_{x\to 0^{+}}(1)=1

como observamos ahora son distintos, significa que el límite cuando \displaystylex \to 0   NO existe, sin embargo la función SÍ esta definida en cero \displaystyle f(x)=0 , recalcando que el límite es un concepto distinto a la evaluación.

Límite infinito

Definimos:

\displaystyle \lim_{x\to a}f(x)=+\infty

1Compruebe que

\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+\infty

Solución:

Primero observemos la gráfica de la función

grafica del reciproco de la x cuadrada

aquí notamos claramente que cuando \displaystyle x \to 0 , la función\displaystyle \frac{1}{x^2} crece indeterminadamente, es decir \displaystyle \frac{1}{x^2} \to \infty

Demostremos.

Sea 0″> cualquier valor real positivo no cero, existe 0″>  tal que, para todo\displaystyle x si

entonces, quitando al cero

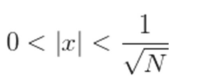
elevando al cuadrado

quitando la raíz

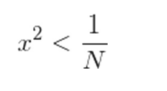
reestructurando

concluyendo

\displaystyle \frac{1}{x^2}>N

llegando así a la demostración del límite

Límite menos infinito

Definimos:

2Compruebe que

\displaystyle \lim_{x \to 0}\left (-\frac{1}{x^2} \right )=-\infty

Solución:

Primero observemos la gráfica de la función

grafica de limite al menos infinito

aquí notamos claramente que cuando \displaystyle x \to 0, la función \displaystyle \frac{-1}{x^2}  decrece indeterminadamente, es decir \displaystyle -\frac{1}{x^2} \to -\infty

Demostremos

entonces, quitando al cero

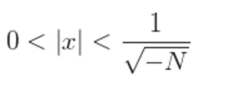
elevando al cuadrado

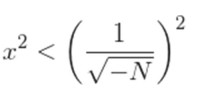
quitando la raíz

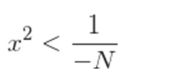
reestructurando

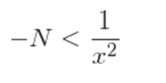
concluyendo

llegando así a la demostración del límite

Límite cuando x tiende a infinito

El límite de una función {f(x)} cuando {x\to\infty} puede tener los siguientes resultados:

1 Una constante {k\in\mathbb{R}}

Se debe satisfacer lo siguiente:

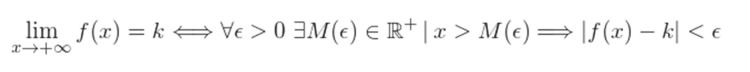
2 Infinito positivo {+\infty}

Se debe satisfacer lo siguiente:

{\displaystyle\lim_{x\to +\infty}f(x)=+\infty \Longleftrightarrow \forall P\in\mathbb{R}^{+} \; \exists M(P)\in \mathbb{R}^{+} \, | \, x>M(P) \Longrightarrow f(x)>P}

3 Infinito negativo {-\infty}

Se debe satisfacer lo siguiente:

Límite cuando x tiende a menos infinito

El límite de una función {f(x)} cuando {x\to -\infty} puede tener los siguientes resultados:

1 Una constante {k\in\mathbb{R}}

Se debe satisfacer lo siguiente:

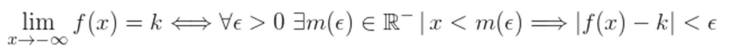
2 Infinito positivo {+\infty}

Se debe satisfacer lo siguiente:

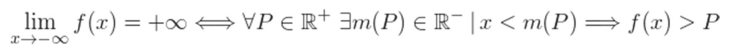
3 Infinito negativo {-\infty}

Se debe satisfacer lo siguiente:

Ejemplos de funciones con límites al infinito

1 Hallar los límites cuando {x \to \pm\infty} para la función {f(x)=\displaystyle\frac{x+1}{x-1}}.

Graficamos la función

grafica de limites en el infinito

A partir de la gráfica obtenemos

{\displaystyle\lim_{x\to +\infty}\frac{x+1}{x-1}=1}
{\displaystyle\lim_{x\to -\infty}\frac{x+1}{x-1}=1}

2 Hallar los límites cuando {x \to \pm\infty} para la función {f(x)=\displaystyle\frac{x^{2}}{x-1}}.

Graficamos la función

representacion grafica de funcion con limites en el infinito

A partir de la gráfica obtenemos

{\displaystyle\lim_{x\to +\infty}\frac{x^{2}}{x-1}=+\infty}
{\displaystyle\lim_{x\to -\infty}\frac{x^{2}}{x-1}=-\infty}

3 Hallar los límites cuando {x \to \pm\infty} para la función {f(x)=\displaystyle\frac{-x^{2}}{x-1}}.

Graficamos la función

dibujo de grafica de una funcion con limites que tienden al infinito

A partir de la gráfica obtenemos

{\displaystyle\lim_{x\to +\infty}\frac{-x^{2}}{x-1}=-\infty}
{\displaystyle\lim_{x\to -\infty}\frac{-x^{2}}{x-1}=+\infty}

Propiedades de los límites

Límite de una constante

\displaystyle \lim_{x\rightarrow a}k=k

Límite de una suma

\displaystyle \lim_{x\rightarrow a}[f(x)\pm g(x)]=\lim_{x\rightarrow a}f(x)\pm \lim_{x\rightarrow a}g(x)

Límite de un producto

\displaystyle \lim_{x\rightarrow a}[f(x)\cdot g(x)]=\lim_{x\rightarrow a}f(x)\cdot \lim_{x\rightarrow a}g(x)

Límite de un cociente

\displaystyle \lim_{x\rightarrow a} \left [\displaystyle \frac{f(x)}{g(x)} \right ]=\frac{\lim_{x\rightarrow a}f(x)}{\lim_{x\rightarrow a}g(x)} \ \ \ \ \ \ \ \ \ \ \ si \ \ \ \ \\lim_{x\rightarrow a}g(x)\neq 0

Límite de una potencia

\displaystyle \lim_{x\rightarrow a}\left [ f(x)^{g(x)} \right ]=\lim_{x\rightarrow a}\left [ f(x) \right ]^{\lim_{x\rightarrow a} g(x)} \ \ \ \ \ \ \ \ \ \ \ si \ \ \ \ \ f(x)> 0

Límite de una función

\displaystyle \lim_{x\rightarrow a} g\left [ f(x) \right ]=g \lim_{x\rightarrow a}f(x)

g puede ser una raíz, un log, sen ,cos, tg, etc.

Límite de una raíz

\displaystyle \lim_{x\rightarrow a} \sqrt[n]{f(x)}=\sqrt[n]{\lim_{x\rightarrow a}f(x)} \ \ \ \ \ Si \ n \ es \ impar \ \ \ \ \ f(x)\geq 0 \ \ \ \ \ Si \ n \ es \ par

Límite de un logaritmo

\displaystyle \lim_{x\rightarrow a} \left [log_a \ f(x)\right ]=log_a \ \left [ \lim_{x\rightarrow a }f(x ) \right ] \ \ \ \ \ \ \ \ \ \ Si \ a> o \ \ \ y \ \ \ f(x)> 0

Debemos señalar que estas indicaciones no son operaciones propiamente dichas, sino simplemente un recurso para ayudarnos a resolver límites.

Debemos tener claro que infinito no es un número.

No distinguimos entre +∞ y −∞ para no alargar excesivamente la lista. Nos basta con saber:

Las leyes de los signos y la propiedad del exponente negativo:  a-n = 1/a n

Sumas con infinito

1Infinito más un número

Suma o resta con infinito

2Infinito más infinito

Suma de infinitos

3Infinito menos infinito

Resta de infinitos

Productos con infinito

1Infinito por un número

Producto de un escalar distinto de cero por infinito

2Infinito por infinito

Producto de infinitos

3Infinito por cero

Producto de Cero por infinito

Cocientes con infinito y cero

1Cero partido por un número

cero entre una constante

2Un número partido por cero

Una constante entre cero

3Un número partido por infinito

Razón de una constante entre infinito

4Infinito partido por un número

Razón de infinito entre una constante

5Cero partido por infinito

Razón de cero respecto infinito

6Infinito partido por cero

Infinito dividido entre cero

7Cero partido por cero

Indeterminación al dividir cero entre cero

8Infinito partido por infinito

Indeterminación al dividir infinitos

Potencias con infinito y cero

1Un número elevado a cero

Potencia cero en una constante

2Cero elevado a cero

Potencia cero en el cero

3Infinito elevado a cero

Potencia cero en el infinito

4Cero elevado a un número

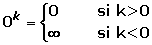
Potencia constante en el cero

5Un número elevado a infinito

Potencia infinita en una constante

6Cero elevado a infinito

Potencia infinita en el cero

7Infinito elevado a infinito

Potencia infinita en el infinito

8Uno elevado a infinito

Potencia infinita en el 1

Cálculo del límite en un punto

Si f(x) es una función común (polinómica, racional, radical, exponencial, logarítmica, etc.) y está definida en el punto a, entonces se puede expresar como:

\lim_{x\to&a}f(x)=f(a)

Es decir, para calcular el límite de la función f(x) se sustituye el valor al que tiende x\rightarrow&space;a$" alt="$x\rightarrow a, como se observa en las siguientes expresiones:

ejemplo calculo limite funcion
ejemplo funcion y calculo limite
ejemplo funcion y calculo de limite

Note que, no podemos calcular \lim_{x\to-2}{\sqrt_{x}}  porque su dominio por definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a −2.

Sin embargo, sí es posible calcular el siguiente límite:

ejemplo calculo limite fraccion

porque aunque 3 no pertenezca al dominio, D= ℛ − {2, 3}, sí podemos tomar valores del dominio tan próximos a 3 como queramos.

Cálculo del límite de una función definida en intervalos

En primer lugar para determinar el límite de una función definida en trozos tenemos que estudiar los límites laterales en los puntos de unión de los diferentes intervalos, si coinciden, será este es el valor del límite, pero si no coinciden, el límite no existe.

En la siguiente función tenemos que:

funcion definida en intervalos

Si, estudiamos los límites laterales en x = −1, tenemos que:

  1. Por la izquierda: limite lateral ejemlo
  2. Por la derecha:ejemplo de limite lateral

Como en ambos casos el límite coincide, el límite existe y vale 1.

En el caso de  x = 1, los límites laterales son:

  1. Por la izquierda: Ejemplo de limite lateral de una funcion
  2. Por la derecha: El limite lateral de una funcion definida en intervalos

Como podrá observar en este caso no coinciden los límites laterales, por lo tanto f(x) no tiene límite en x = 1.

De forma intuitiva, podemos decir que para calcular un límite de la forma

\displaystyle \lim_{x \to \infty}{f(x)}

La manera de hacerlo es sustituyendo la x por \infty.

Sin embargo, este procedimiento puede que no funcione siempre, pues en algunas situaciones no es claro el valor que tomará la función cuando se evalúa en \infty. Describimos abajo algunas de las situaciones en las que no es claro el valor del límite y cómo determinarlo:

Límite de funciones polinómicas en el infinito

Consideremos un polinomio de la forma

\displaystyle P(x) = a_nx^n + a_{n - 1}x^{n - 1} + \cdots + a_1 x + a_0

Entonces, el límite es

En otras palabras, el signo del límite es el mismo que el signo del coeficiente principal del polinomio.

Ejemplos

1. El siguiente límite

\displaystyle \lim_{x \to \infty}{(3x^4 + x^3 - 2x)} = \infty

es \infty debido a que el coeficiente principal (es decir, 3) es positivo.

2. El límite

\displaystyle \lim_{x \to \infty}{(- x^2 + 5x + 6)} = - \infty

toma el valor - \infty debido a que el coeficiente principal es negativo (-1).

Nota: observemos en el ejemplo anterior que sustituir por \infty no nos ayudaría a calcular el límite. Esto debido a que

\begin{align*} \lim_{x \to \infty}{(- x^2 + 5x + 6)} & = -(\infty)^2 + 5(\infty) + 6\\ & = - \infty + \infty + 6\\ & = - \infty + \infty \end{align*}

Es decir, tenemos una indeterminación de la forma \infty - \infty.

Límite de la inversa de un polinomio en el infinito

Si P(x) es un polinomio de grado mayor o igual a 1, entonces el límite de 1/P(x) cuando x \to \infty está dado por

\displaystyle \lim_{x \to \infty}{ \frac{1}{P(x)} } = 0

Por ejemplo, consideremos el siguiente límite,

\displaystyle \lim_{x \to \infty}{\frac{1}{3x^4 + x^3 - 2x} } = 0

Cálculo de límites cuando x tiene a infinito negativo

Para calcular los límites cuando x \to -\infty simplemente nos apoyamos de la propiedad:

\displaystyle \lim_{x \to \infty}{ f(x) } = \lim_{ x \to \infty }{ f(-x) }

De esta manera, el límite cuando x \to -\infty es equivalente a calcular un límite cuando x \to \infty.

Ejemplos

1. Consideremos el límite de 3x^4 + x^3 - 2x cuando x \to \infty. Entonces,

\displaystyle \lim_{x \to -\infty}{(3x^4 + x^3 - 2x)} = \lim_{x \to \infty}{(3x^4 - x^3 + 2x)} = \infty

2.Veamos el siguiente límite

\displaystyle \lim_{x \to -\infty}{(-x^2 + 5x + 6)} = \lim_{x \to \infty}{(-x^2 - 5x + 6)} = - \infty

3. Ahora consideremos el límite con un radical

\begin{align*} \lim_{x \to -\infty}{\sqrt{2x^2 - 8x - 3} } & = \lim_{x \to \infty}{ \sqrt{2(-x)^2 - 8(-x) - 3} }\\ & = \lim_{x \to \infty}{ \sqrt{ 2x^2 + 8x - 3 } }\\ & = \infty \end{align*}

Recordemos que

\displaystyle \lim_{y \to \infty}{\sqrt{y}} = \infty

4. Por último, veamos otro límite con un radical:

\begin{align*} \lim_{x \to - \infty}{\sqrt{x^3 - 5x} } & = \lim_{x \to \infty}{\sqrt{ (-x)^3 - 5(-x) } }\\ & = \lim_{x \to \infty }{ \sqrt{-x^3 + 5x} } \end{align*}

En este caso, el límite no existe porque el radicando toma valores negativos.

Límites de una función exponencial

Caso 1: Si a > 1

grafica de limite de funcion exponencial en infinito 1

De la gráfica podemos observar que

1{\displaystyle\lim_{x\to \infty}a^{x}=\infty}

2{\displaystyle\lim_{x\to -\infty}a^{x}=0}

Caso 2: Si 0 < a < 1

grafica de limite de funcion exponencial en infinito 2

De la gráfica podemos observar que

1{\displaystyle\lim_{x\to \infty}a^{x}=0}

2{\displaystyle\lim_{x\to -\infty}a^{x}=\infty}

Ejemplos

1{\displaystyle\lim_{x\to \infty}3^{x+2}}

Solución:

Aplicamos la siguiente ley de los exponentes: {(ab)^{n}=a^{n}b^{n}}

{\displaystyle\lim_{x\to \infty}3^{x+2}=\lim_{x\to \infty}\left(3^{x}3^{2}\right)

Aplicamos límite a cada elemento del producto y obtenemos

{\displaystyle\lim_{x\to \infty}3^{x+2}=\lim_{x\to \infty}\left(3^{x}3^{2}\right)=\left(\lim_{x\to \infty}3^{2}\right)\left(\lim_{x\to \infty}3^{x}\right)=3^{2}(\infty)=\infty}

2{\displaystyle\lim_{x\to \infty}3^{-x+2}}

Solución:

Aplicamos las siguientes leyes de los exponentes: {(ab)^{n}=a^{n}b^{n} \ \ \ \ a^{-n}=\displaystyle\frac{1}{a^{n}}}

{\begin{array}{rcl} \displaystyle\lim_{x\to \infty}3^{-x+2} &=&\displaystyle\lim_{x\to \infty}\left(3^{-x}3^{2}\right)=\displaystyle\lim_{x\to \infty}\left(\frac{1}{3^{x}}3^{2}\right) \end{array}}

Aplicamos límite a cada elemento del producto

{\begin{array}{rcl} \displaystyle\lim_{x\to \infty}3^{-x+2} &=&\displaystyle\lim_{x\to \infty}\left(3^{-x}3^{2}\right)=\displaystyle\lim_{x\to \infty}\left(\frac{1}{3^{x}}3^{2}\right)=\displaystyle\lim_{x\to \infty}\left(3^{2}\right)\left(\displaystyle\lim_{x\to \infty}\left(\frac{1}{3^{x}}\right)\right) \end{array}}

Aplicamos límite a cada elemento del cociente y obtenemos

{\begin{array}{rcl} \displaystyle\lim_{x\to \infty}3^{-x+2} &=&\displaystyle\lim_{x\to \infty}\left(3^{-x}3^{2}\right)=\displaystyle\lim_{x\to \infty}\left(\frac{1}{3^{x}}3^{2}\right)=\displaystyle\lim_{x\to \infty}\left(3^{2}\right)\left(\displaystyle\lim_{x\to \infty}\left(\frac{1}{3^{x}}\right)\right) \\ && \\ &=&3^{2}\left(\displaystyle\frac{\displaystyle\lim_{x\to \infty}1}{\displaystyle\lim_{x\to \infty}3^{x}}\right)=3^{2}\left(\displaystyle\frac{1}{\infty}\right)=3^{2}(0)=0 \end{array}}

3{\displaystyle\lim_{x\to \infty}\left(\frac{1}{3}\right)^{x+2}}

Solución:

Aplicamos la siguiente ley de los exponentes: {(ab)^{n}=a^{n}b^{n}}

{\displaystyle\lim_{x\to \infty}\left(\frac{1}{3}\right)^{x+2}=\lim_{x\to \infty}\left[\left(\frac{1}{3}\right)^{x}\left(\frac{1}{3}\right)^{2}\right]}

Aplicamos límite a cada elemento del producto y obtenemos

{\displaystyle\lim_{x\to \infty}\left(\frac{1}{3}\right)^{x+2}=\lim_{x\to \infty}\left[\left(\frac{1}{3}\right)^{x}\left(\frac{1}{3}\right)^{2}\right]=\left[ \lim_{x\to \infty}\left(\frac{1}{3}\right)^{2}\right]\left[ \lim_{x\to \infty}\left(\frac{1}{3}\right)^{x}\right]=\left(\frac{1}{3}\right)^{2} (0)=0}

4{\displaystyle\lim_{x\to -\infty}\left(\frac{1}{3}\right)^{x+2}}

Solución:

Aplicamos la siguiente ley de los exponentes: {(ab)^{n}=a^{n}b^{n}}

{\displaystyle\lim_{x\to -\infty}\left(\frac{1}{3}\right)^{x+2}=\lim_{x\to -\infty}\left[\left(\frac{1}{3}\right)^{x}\left(\frac{1}{3}\right)^{2}\right]}

Aplicamos límite a cada elemento del producto y obtenemos

{\displaystyle\lim_{x\to -\infty}\left(\frac{1}{3}\right)^{x+2}=\lim_{x\to -\infty}\left[\left(\frac{1}{3}\right)^{x}\left(\frac{1}{3}\right)^{2}\right]=\left(\frac{1}{3}\right)^{2}\left[ \lim_{x\to -\infty}\left(\frac{1}{3}\right)^{x}\right]=\left(\frac{1}{3}\right)^{2} (\infty)=\infty}

Límite de la función logarítmica

Caso 1: Si a > 0

Para la función f(x)=a^{x} con  0″> se tiene una función creciente con dominio D=(0,\infty ) y asintota horizontal en x=0:

Gráfica de una función logarítmica con base mayor a uno
\displaystyle \lim_{x \to \infty }\log_{a}x=\infty
\displaystyle \lim_{x \to 0^{+}}\log_{a}x=-\infty

Caso 2: Si 0 < a < 1

Gráfica de una función logarítmica con base menor a uno
\displaystyle \lim_{x \to 0^{+}}\log_{a}x=\infty
\displaystyle \lim_{x \to \infty }\log_{a}x=-\infty

Ejemplo

Estudiar la función: f(x)=\log(x^{2}-9)

1 Calculamos el dominio de la función resolviendo la desigualdad:

x^{2}-9> 0

2 Para verificar las asintotas, calculamos los siguiente limites:

D=(-\infty ,-3)\cup (3,\infty )
\displaystyle \lim_{x \to -\infty }\log(x^{2}-9)=\lim_{x \to -\infty }\log\left [ (-x)^{2}-9 \right ]=\log\left [\lim_{x \to -\infty }(x^{2}-9) \right ]
=\log\infty =\infty
\displaystyle\lim_{x\to -3^{-}}\log(x^{2}-9)=\log\left [ \lim_{x\to -3^{-}}(x^{2}-9) \right ]=\log 0^{+}=-\infty
\displaystyle \lim_{x \to 0}\log(x^{2}-9)=\log\left [ \lim_{x\to 0}(x^{2}-9) \right ]=\log(-9)\; \; \; \; \; \; \; \; \; \; \textup{No existe}
\displaystyle\lim_{x\to3^{+}}\log(x^{2}-9)=\log\left [ \lim_{x\to 3^{+}}(x^{2}-9) \right ]=\log 0^{+}=-\infty
\displaystyle \lim_{x\to \infty }\log(x^{2}-9)=\log\left [ \lim_{x\to \infty }(x^{2}-9) \right ]=\log \infty =\infty
Ejemplo de limites en una función logarítmica representación gráfica

Indeterminaciones – 7 tipos

Una indeterminación no significa que el límite no exista o no se pueda determinar, sino que la aplicación de las propiedades de los límites tal como las hemos enunciado no son válidas.

En estos casos hay que efectuar operaciones particulares para resolver cada una de las indeterminaciones.

Da click en cada una de las indeterminaciones para encontrar ejemplos de cómo tratarlas:

1 Infinito partido por infinito

\cfrac{\infty }{\infty }

2 Cero partido cero

\cfrac{0 }{0 }

3 Cero por infinito

0\cdot {\infty }

4 Cero elevado a cero

0^{0}

5 Infinito elevado a cero

\infty ^{0}

6 Uno elevado a infinito

1^{\infty }

7 Infinito menos infinito

{\infty }-{\infty }

Cociente de límites en el infinito por comparación

Si {\displaystyle\lim_{x \to \infty}f(x)= \pm\infty} y {\displaystyle\lim_{x \to \infty}g(x)= \pm\infty}, entonces se tienen los siguientes resultados para el cociente de funciones:

1Si {f(x)} es un infinito de orden superior a {g(x)}, entonces

{\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)}= \pm\infty}

2.Si {f(x)} es un infinito de orden inferior a {g(x)}, entonces

{\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)}= 0}

3.Si {f(x)} es un infinito de igual orden a {g(x)}, entonces el cociente es igual a una constante diferente de cero

{\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)}= c \neq 0}

Comparación de funciones en infinito

1Dadas dos potencias de {x}, la de mayor exponente es un infinito de orden superior.

2Dadas dos funciones exponenciales de base mayor que 1, la de mayor base es un infinito de orden superior.

3Cualquier función exponencial de base mayor que 1 es un infinito de orden superior a cualquier potencia de {x}.

4Las potencias de {x} son infinitos de orden superior a las funciones logarítmicas.

5Dos polinomios del mismo grado o dos exponenciales de la misma base son infinitos del mismo orden.

Ejemplos de ejercicios por comparación de infinitos

Hallar los límites por comparación de infinitos:

1{\displaystyle\lim_{x \to \infty}\left( \frac{e^{x}}{x^{25}-25} \right)= \infty}

En este ejemplo tenemos que

{f(x)=e^{x}}
{g(x)=x^{25}-25}

El resultado se obtiene a partir de la propiedad de que cualquier función exponencial de base mayor que 1 es un infinito de orden superior a cualquier potencia. Así {f(x)} es un infinito de orden superior a {g(x)}

2{\displaystyle\lim_{x \to \infty}\left( \frac{\sqrt{x^{7}-7}}{x^{3}-3} \right)= \infty}

En este ejemplo tenemos que

{f(x)=\sqrt{x^{7}-7}}
{g(x)=x^{3}-3}

El resultado se obtiene a partir de la propiedad de que la función de mayor exponente es un infinito de orden superior. Así {f(x)} es un infinito de orden superior a {g(x)}

3{\displaystyle\lim_{x \to \infty} \left[\frac{log\left( x^{34}-56\right)}{2x^{2}} \right]= 0}

En este ejemplo tenemos que

{f(x)=log\left( x^{34}-56\right)}
{g(x)=2x^{2}}

El resultado se obtiene a partir de la propiedad de que las potencias de {x} son infinitos de orden superior a las funciones logarítmicas. Así {f(x)} es un infinito de orden inferior a {g(x)}

¿Qué forma tienen los límites de un número partido por cero?

Estos límites son de la forma {\displaystyle\frac{k}{0}} para {k\neq 0}

El límite puede ser {+\infty,\ \ \ -\infty} o      no tener límite.

Ejemplos de cálculo de límites de un número partido por cero

Calcular el límite:

1 {\displaystyle\lim_{x\to -1}\frac{x-1}{x+1}=\frac{-2}{0}}

Este límite es de la forma {\displaystyle\lim_{x\to -1}\frac{x-1}{x+1}=\frac{-2}{0}}. Tomamos los límites laterales para determinar el signo de {\infty}.

Si le damos a la {x} un valor que se acerque a −1 por la izquierda como −1.1; tanto el numerador como denominador son negativos, por tanto el límite por la izquierda será: {+\infty}

{\displaystyle\lim_{x\to -1^{-}}\frac{x-1}{x+1}=\frac{(-)}{(-)}=\infty}

Si le damos a la {x} un valor que se acerque a −1 por la derecha como −0.9. El numerador será negativo y el denominador positivo, por tanto el límite por la derecha será: {-\infty}.

{\displaystyle\lim_{x\to -1^{+}}\frac{x-1}{x+1}=\frac{(-)}{(+)}=-\infty}

Como no coinciden los límites laterales, la función no tiene límite cuando {x\to -1}.

2 {\displaystyle\lim_{x\to 0}\frac{1}{x}}

Este límite es de la forma {\displaystyle\lim_{x\to 0}\frac{1}{x}=\frac{1}{0}}. Tomamos los límites laterales para determinar el signo de {\infty}.

{\displaystyle\lim_{x\to 0^{-}}\frac{1}{x}=\frac{(+)}{(-)}=-\infty}
{\displaystyle\lim_{x\to 0^{+}}\frac{1}{x}=\frac{(+)}{(+)}=\infty}

Como no coinciden los límites laterales la función no tiene límite cuando {x\to 0}

3 {\displaystyle\lim_{x\to 0}\frac{1}{x^{2}}}

Este límite es de la forma {\displaystyle\lim_{x\to 0}\frac{1}{x^{2}}=\frac{1}{0}}. Tomamos los límites laterales para determinar el signo de {\infty}.

{\displaystyle\lim_{x\to 0^{-}}\frac{1}{x^{2}}=\frac{(+)}{(+)}=\infty}
{\displaystyle\lim_{x\to 0^{+}}\frac{1}{x^{2}}=\frac{(+)}{(+)}=\infty}

Como coinciden los límites laterales la función tiene límite {\infty} cuando {x\to 0}

4 {\displaystyle\lim_{x\to 0}\frac{-1}{x^{2}}}

Este límite es de la forma {\displaystyle\lim_{x\to 0}\frac{1}{x^{2}}=-\frac{1}{0}}. Tomamos los límites laterales para determinar el signo de {\infty}.

{\displaystyle\lim_{x\to 0^{-}}\frac{-1}{x^{2}}=\frac{(-)}{(+)}=-\infty}
{\displaystyle\lim_{x\to 0^{+}}\frac{-1}{x^{2}}=\frac{(-)}{(+)}=-\infty}

Como coinciden los límites laterales la función tiene límite {-\infty} cuando {x\to 0}

Indeterminación infinito dividido por infinito

En ocasiones nos encontramos con que una función tiene una indeterminación de infinito dividido por infinito. Es decir, consideremos la función

\displaystyle f(x) = \frac{g(x)}{h(x)}

tal que \lim_{x \to a}{g(x)} = \infty \; y \;\lim_{x \to a}{h(x)} = \infty. Así, nuestra función evaluada en a sería

\displaystyle f(a) = \frac{g(a)}{h(a)} = \frac{\infty}{\infty}

En este caso, decimos que la función está indeterminada en a, pues no es posible asignarle valor alguno a f(a). Sin embargo, podemos utilizar alguno de los siguientes dos métodos para encontrar el límite de la función en a —observemos que el límite en a no es lo mismo que el valor de f(a)—:

Primer método: comparación del orden de los polinomios

Estos métodos sólo funcionan con funciones racionales de la forma

\displaystyle f(x) = \frac{P(x)}{Q(x)}

en donde P(x) y Q(x) son polinomios y algunos casos muy particulares como exponenciales y radicales. Cuando no se tienen estos casos, existen otros métodos como la regla de L’Hôpital.

El primer método consiste en comparar los grados de P(x) y Q(x):

El numerador tiene mayor grado que el denominador

Si el numerador P(x) tiene mayor grado que el denominador, entonces el límite será +\infty o -\infty. El signo del límite será el mismo signo que tiene la división de los coeficientes de mayor grado. En el segundo ejemplo de abajo, observemos que el límite es -\infty porque la división de los coeficientes es (-2)/1 = -2; es decir, tiene signo negativo.

\begin{align*} & \lim_{x \to \infty}{ \frac{2x^5 - 3x^2}{x^4 - x^3} } = \infty\\[8pt] & \lim_{x \to \infty}{\frac{-2x^5 - 3x^2}{x^4 - x^3}} = -\infty \end{align*}

El grado del denominador es mayor al grado del numerador

Si el grado del denominador Q(x) es mayor al grado del numerador, entonces el límite siempre será 0. 

\displaystyle \lim_{x \to \infty}{ \frac{2x^5 - 3x^2}{x^7 - x^3} } = 0

El numerador y el denominador tienen el mismo grado

Si el numerador y denominador tienen el mismo grado, entonces el límite es el cociente de los coeficientes de mayor grado. Observemos el ejemplo de abajo. El numerador tiene coeficiente principal 2, mientras que el denominador tiene coeficiente principal 3. Por lo tanto, como ambos polinomios tienen el mismo grado, entonces el límite es 2/3.

\displaystyle \lim_{x \to \infty}{\frac{2x^5 - 3x^2}{3x^5 - x^3}} = \frac{2}{3}

Casos particulares del método de comparación

Dada una función

\displaystyle f(x) = \frac{g(x)}{h(x)}

existen casos donde podemos comparar a g(x) y h(x) de manera similar a como comparamos los polinomios. Estos casos involucran funciones exponenciales y funciones radicales.

1 Si g(x) o h(x) son exponenciales, entonces podemos pensar que su grado siempre es mayor al de cualquier polinomio (formalmente se dice que una exponencial es de mayor orden que un polinomio). Si tanto el numerador como el denominador son exponenciales, entonces tendrá mayor orden la exponencial con la base más grande.

\begin{align*} & \lim_{x \to \infty}{ \frac{2x^5 - 3x^2}{6^x} } = 0\\[8pt] & \lim_{x \to \infty}{\frac{3^x}{x^4 - x^3}} = \infty\\[8pt] & \lim_{x \to \infty}{\frac{3^x}{4^x}} = 0\end{align*}

2 Si el numerador o el denominador es un radical de la forma

\sqrt[m]{a_n x^n + a_{n-1} x^{n - 1} + \cdots},

entonces consideramos que su grado es n/m y su coeficiente de mayor grado es \sqrt[m]{a_n}.

\begin{align*} & \lim_{x \to \infty}{ \frac{2x^3 - 3x^2}{\sqrt[3]{6x^2 + 1}} } = \infty\\[8pt] & \lim_{x \to \infty}{\frac{\sqrt{3x^2 + 4}}{\sqrt{2x^2 + 1}}} = \frac{\sqrt{3}}{\sqrt{2}}\end{align*}

Segundo método: dividir por una misma función el numerador y denominador

Dado que

\displaystyle 1 = \frac{P(x)}{P(x)}

entonces podemos multiplicar y dividir una función por P(x) con el fin de calcular el límite de forma más sencilla. Esto debido a que

\displaystyle f(x) = \frac{g(x)}{h(x)} \cdot 1 = \frac{g(x)}{h(x)} \cdot \frac{P(x)}{P(x)} = \frac{g(x)P(x)}{h(x)P(x)}

Cociente de polinomios

Si se trata de cociente de polinomios, entonces dividimos ambos polinomios por la potencia de mayor grado. Por ejemplo, si tenemos

\displaystyle \lim_{x \to \infty}{\frac{2x^5 - 3x^2}{x^4 - x^3}} = \frac{\infty}{\infty}

Dividimos cada polinomio por x^5, simplificamos las fracciones y aplicamos el límite:

\displaystyle \lim_{x\to \infty}{ \frac{ \frac{2x^5}{x^5} - \frac{3x^2}{x^2} }{ \frac{x^4}{x^5} - \frac{x^3}{x^5} } } = \frac{ \lim_{x \to \infty}{ 2 - \frac{3}{x^3} } }{ \lim_{x \to \infty}{ \frac{1}{x} - \frac{1}{x^2} } } = \frac{2 - 0}{0 - 0} = \infty

Es importante que tomemos en cuenta el signo de los coeficientes de mayor grado del numerador y denominador, pues esto puede cambiar el signo del infinito. Al igual que con el método anterior, el signo será el mismo que el cociente de los coeficientes de mayor grado.

Funciones exponenciales

Si son funciones exponenciales, entonces dividimos por la exponencial de mayor base. Observemos el siguiente ejemplo: 

\displaystyle \lim_{x \to \infty}{ \frac{3^{x +2} + 2^x}{3^{x-2}} } = \frac{\infty}{\infty}

Primero aplicamos las propiedades del producto y del cociente de potencias, con el fin de quitar las sumas o restas de los exponentes:

\displaystyle \lim_{x \to \infty}{\frac{3^x \cdot 3^2 + 2^x}{3^x \cdot 3^{-2}} }

Dividimos el numerador y el denominador por 3 a la equis

\displaystyle \lim_{x \to \infty}{ \frac{3^{x +2} + 2^x}{3^{x-2}} } = \lim_{x \to \infty}{\frac{ \frac{3^x \cdot 3^2}{3^x} + \frac{2^x}{3^x} }{ \frac{3^x \cdot 3^{-2}}{3^x} } } = \frac{9 + 0}{\frac{1}{9}} = 81

Ejemplos de la indeterminación infinito dividido por infinito

Vamos a resolver algunos ejemplos para poner en práctica lo que acabamos de ver.1\displaystyle \lim_{x \to \infty}{ \frac{3^x}{2^x}} = \infty

El resultado es \infty ya que el numerador es de orden mayor que el denominador.2\displaystyle \lim_{x \to \infty}{ \frac{2^x}{3^x}} = 0

Ahora tenemos un denominador con orden superior al del numerador. Por lo tanto, el límite es 0.3\displaystyle \lim_{x \to \infty}{ \frac{\sqrt{x^7 - 2} }{ x^4 - 1} } = 0

En este caso tenemos una función radical en el numerador. Por lo tanto, suponemos que su grado es 7/2. Por consiguiente, debido a que  7/2″>, entonces el límite es 0.4\displaystyle \lim_{x \to \infty}{ \frac{2^x}{x^23} } = \infty

Como mencionamos anteriormente, las funciones exponenciales siempre tienen mayor orden que los polinomios —aunque este sea de grado 23—. Por tanto, el límite es \infty.

Infinito menos infinito

Para resolver la indeterminación 

{\infty - \infty}

 tenemos varios métodos:

1. Por comparación de infinitos

Ejemplo:

{\displaystyle\lim_{x \to \infty}(x^{7}-x^{5}+x^{3}-x^{2})=\infty}

Se obtiene por tener {x^{7}} el mayor orden.

Ejemplo:

{\displaystyle\lim_{x \to \infty}\left(x^{2}-\sqrt{x+3}\right)=\infty}

Se obtiene por tener {x^{2}} el mayor orden.

Ejemplo:

{\displaystyle\lim_{x \to \infty}\left(x^{2}-\sqrt{x^{5}+3}\right)=-\infty}

Se obtiene puesto que 2}»> .

Ejemplo:

{\displaystyle\lim_{x \to \infty}\left(3^{x}-\sqrt{x^{8}-2}\right)=\infty}

Se obtiene por tener {3^{x}} el mayor orden.

2. Con funciones racionales

Ejemplo:

{\displaystyle\lim_{x \to 3}\left( \frac{x-1}{x-3}-\frac{x+5}{x^2-4x+3} \right)}

1El límite anterior posee la indeterminación {\infty-\infty}

2Realizamos la suma de fracciones para tener un común denominador.

{\displaystyle\lim_{x \to 3}\left( \frac{x-1}{x-3}-\frac{x+5}{x^2-4x+3} \right)=\displaystyle\lim_{x \to 3}\frac{x^{2}-3x-4}{(x-3)(x-1)}}

3Observamos que el denominador se aproxima a cero cuando {x \to 3}, mientras que el numerador se aproxima a {-4}; por ello debemos proceder mediante límites laterales.

4Calculamos los límites laterales

{\displaystyle\lim_{x \to 3^{-}}\left( \frac{x-1}{x-3}-\frac{x+5}{x^2-4x+3} \right)=\displaystyle\lim_{x \to 3^{-}}\frac{x^{2}-3x-4}{(x-3)(x-1)}=\infty}
{\displaystyle\lim_{x \to 3^{+}}\left( \frac{x-1}{x-3}-\frac{x+5}{x^2-4x+3} \right)=\displaystyle\lim_{x \to 3^{+}}\frac{x^{2}-3x-4}{(x-3)(x-1)}=-\infty}

5Por el teorema de los Límites Laterales concluimos que

{\displaystyle\lim_{x \to 3}\left( \frac{x-1}{x-3}-\frac{x+5}{x^2-4x+3} \right)=\nexists}

3. Con funciones irracionales

Ejemplo:

{\displaystyle\lim_{x \to \infty}\left( \sqrt{x^{2}-2}-\sqrt{x^2+x} \right)}

1El límite anterior posee la indeterminación {\infty-\infty}

2Cuando se trata de funciones irracionales podemos multiplicar y dividir por el conjugado.

{\displaystyle\lim_{x \to \infty}\left( \sqrt{x^{2}-2}-\sqrt{x^2+x} \right)=\lim_{x \to \infty}\frac{\left( \sqrt{x^{2}-2}-\sqrt{x^2+x} \right)\left( \sqrt{x^{2}-2}+\sqrt{x^2+x} \right)}{\sqrt{x^{2}-2}+\sqrt{x^2+x}}}

3En el numerador tenemos una suma por diferencia que es igual a diferencia de cuadrados

{\begin{array}{rcl} \displaystyle\lim_{x \to \infty}\left( \sqrt{x^{2}-2}-\sqrt{x^2+x} \right) & = &\displaystyle\lim_{x \to \infty}\frac{\left( \sqrt{x^{2}-2}-\sqrt{x^2+x} \right)\left( \sqrt{x^{2}-2}+\sqrt{x^2+x} \right)}{\sqrt{x^{2}-2}+\sqrt{x^2+x}} \\ && \\ & = &\displaystyle\lim_{x \to \infty}\frac{x^{2}-2-x^{2}-x}{\sqrt{x^{2}-2}+\sqrt{x^2+x}} \\ && \\ & = &\displaystyle\lim_{x \to \infty}\frac{-2-x}{\sqrt{x^{2}-2}+\sqrt{x^2+x}} \\ \end{array}}

4Observamos que cuando {x \to \infty}, el numerador se aproxima a cuando {-\infty}  mientras que el denominador se aproxima a cuando {\infty}.

5Para resolver la indeterminación dividimos todos los sumandos por la {x} de mayor grado, que fuera de la raíz es {x} y al introducirla en la raíz cuadrada será {x^{2}}

{\begin{array}{rcl} \displaystyle\lim_{x \to \infty}\frac{-2-x}{\sqrt{x^{2}-2}+\sqrt{x^2+x}} & = & \displaystyle\lim_{x \to \infty}\frac{\displaystyle\frac{-2}{x}-\displaystyle\frac{x}{x}}{\sqrt{\displaystyle\frac{x^{2}}{x^{2}}-\displaystyle\frac{2}{x^{2}}}+\sqrt{\displaystyle\frac{x^2}{x^{2}}+\displaystyle\frac{x}{x^{2}}}} \\ &=&\\ &=& \displaystyle\frac{-1}{1+1} &=&\\ &=& \displaystyle\frac{-1}{2} \end{array}}

Indeterminación cero sobre cero

Vamos a estudiar la indeterminación del tipo cero partido cero en dos casos.

Caso 1: Función racional

Este caso aplica cuando tenemos una fracción donde el numerador y el denominador son polinomios.

A continuación se explican el procedimiento para obtener el límite cuando tienes una indeterminación del tipo cero entre cero.

1 Al intentar calcular el límite, se identifica la indeterminación del tipo cero sobre cero

2 Se descomponen en factores los polinomios de el numerador y denominador

3 Se simplifica la fracción

4 Se calcula el límite de la expresión simplificada

Ejemplos

  • \displaystyle \lim_{x\rightarrow -1}\frac{x^2+2x+1}{x^2-1}

Solución

1 Si intentamos obtener el límite, veremos que es del tipo 0/0

\displaystyle \lim_{x\rightarrow -1}\frac{x^2+2x+1}{x^2-1}=\frac{(-1)^2+2\cdot (-1)+1}{(-1)^2-1}=\frac{1-2+1}{1-1}=\frac{0}{0}

2 Factorizamos

El numerador es un trinomio cuadrado perfecto que lo podemos escribirlo como un binomio al cuadrado.

El denominador es una diferencia de cuadrados que es igual al producto de binomios conjugados. Esto es

\displaystyle \lim_{x\rightarrow -1}\frac{x^2+2x+1}{x^2-1}=\lim_{x\rightarrow -1} \frac{(x+1)^2}{(x+1)(x-1)}

3 Simplificamos la fracción

\displaystyle \lim_{x\rightarrow -1} \frac{(x+1)^{\cancel{2}}}{\cancel{(x+1)}(x-1)}=\lim_{x\rightarrow -1} \frac{x+1}{x-1}

4 Ahora calculamos el límite

\displaystyle \lim_{x\rightarrow -1} \frac{x+1}{x-1}=\frac{-1+1}{-1-1}=\frac{0}{-2}=0

El límite es 0

  • \displaystyle \lim_{x\rightarrow -1}\frac{x^2-1}{x^2+2x+1}

Solución

1 Si intentamos obtener el límite, veremos que es del tipo 0/0

\displaystyle \lim_{x\rightarrow -1}\frac{x^2-1}{x^2+2x+1}=\frac{(-1)^2-1}{(-1)^2+2(-1)+1}=\frac{1-1}{1-2+1}=\frac{0}{0}

2Factorizamos

El numerador es una diferencia de cuadrados que es igual al producto de binomios conjugados.

El denominador es un trinomio cuadrado perfecto que lo podemos escribirlo como un binomio al cuadrado. Esto es

\displaystyle \lim_{x\rightarrow -1}\frac{x^2-1}{x^2+2x+1}=\lim_{x\rightarrow -1} \frac{(x+1)(x-1)}{(x+1)^2}

3 Simplificamos la fracción

\displaystyle \lim_{x\rightarrow -1} \frac{\cancel{(x+1)}(x-1)}{(x+1)^{\cancel{2}}}=\lim_{x\rightarrow -1} \frac{x-1}{x+1}

4 Ahora calculamos el límite

\displaystyle \lim_{x\rightarrow -1} \frac{x-1}{x+1}=\frac{-1-1}{0}=\frac{-2}{0}

Como obtuvimos cero solamente en el denominador, debemos identificar si este límite va a infinito positivo, negativo o no tiene límite (por un lado se va a infinito positivo y por el otro, negativo). Para esto tomamos límites laterales

Límite por la izquierda

Si le damos a la x un valor que se acerque a -1 por la izquierda como -1.1; tanto el numerador como denominador son negativos, por tanto el límite por la izquierda será: +\infty

\displaystyle \frac{-1.1-1}{-1.1+1}=\frac{-2.1}{-0.1}=21
\displaystyle \lim_{x\rightarrow -1^-} \frac{x-1}{x+1}=\infty

Límite por la derecha

Si le damos a la x un valor que se acerque a −1 por la derecha como −0,9. El numerador será negativo y el denominador positivo, por tanto el límite por la derecha será: -\infty

\displaystyle \frac{-0.9-1}{-0.9+1}=\frac{-1.9}{0.1}=-19
\displaystyle \lim_{x\rightarrow -1^-} \frac{x-1}{x+1}=-\infty

Como el límite por la izquierda y derecha no son iguales se concluye que no existe el límite en x = −1

Caso 2: Función con radicales

Este caso aplica cuando tenemos una fracción que tiene un radical, generalmente en el denominador.

A continuación se explica el procedimiento para obtener el límite cuando tienes una indeterminación del tipo cero entre cero.

1 Al intentar calcular el límite, se identifica la indeterminación del tipo cero sobre cero

2 Multiplicamos numerador y denominador por el conjugado de la expresión irracional.

\begin{matrix} \text{Expresi\'on} & \text{Conjugado}\\ a+\sqrt{b} & a-\sqrt{b}\\ a-\sqrt{b} & a+\sqrt{b} \end{matrix}

Ejemplo:

\begin{matrix} \text{Expresi\'on} & & \text{Conjugado}\\ \\ 3+\sqrt{7} & & 3-\sqrt{7}\\ \\ 2x-5\sqrt{x^2-1} & & 2x+5\sqrt{x^2-1} \end{matrix}

3 Se realizan las operaciones y se simplifica la fracción

Toma en cuenta que una expresión irracional multiplicada por su conjugado, da como resultado una diferencia de cuadrados

(a+\sqrt{b})(a-\sqrt{b})=a^2-b

Ejemplo:

  • (3+\sqrt{5})(3-\sqrt{5})=9-5
  • (\sqrt{2}+\sqrt{5})(\sqrt{2}-\sqrt{5})=2-5
  • (1+3\sqrt{5})(1-3\sqrt{5})=1-9\cdot 5=1-45

4 Se calcula el límite de la expresión simplificada

Ejemplo

  • \displaystyle \lim_{x\rightarrow 0}\frac{x}{1-\sqrt{1-x}}

Solución

1Al intentar calcular el límite, se identifica la indeterminación del tipo cero sobre cero

\displaystyle \lim_{x\rightarrow 0}\frac{x}{1-\sqrt{1-x}}

2Multiplicamos y dividimos por el conjugado del denominador

\displaystyle \lim_{x\rightarrow 0}\frac{x(1+\sqrt{1-x})}{(1-\sqrt{1-x})(1+\sqrt{1-x})}

3Realizamos las operaciones y simplificamos la fracción.

En el denominador tenemos una suma por diferencia (binomios conjugados) que será igual a diferencia de cuadrados

\displaystyle \lim_{x\rightarrow 0}\frac{x(1+\sqrt{1-x})}{1-(1-x)}=\lim_{x\rightarrow 0}\frac{\cancel{x}(1+\sqrt{1-x})}{\cancel{x}}=\lim_{x\rightarrow 0} 1+\sqrt{1-x}

4Calculamos el límite

\displaystyle \lim_{x\rightarrow 0} 1+\sqrt{1-x}=1+\sqrt{1-0}=2

El límite es 2

Indeterminación en el exponente de 1

El objetivo de esta sección es encontrar el límite de funciones que se indeterminan de la forma \displaystyle 1^\infty.

Recordemos que el número de euler \displaystyle e = 2.718281828459...   es el valor a quien converge el siguiente límite:

\displaystyle \lim_{x \to \infty} \left( 1 + \frac{1}{x} \right)^{x} =e

Mostraremos dos métodos para resolver los límites mencionados.

Primer método de resolución de la indeterminación

La idea es resolver el siguiente límite usando el resultado anterior y cierto proceso.

\displaystyle \lim_{x \to 1^{+}} \left(\frac{2x + 1}{x+2} \right)^{\frac{1}{x-1}}

1 Para comenzar notemos que el  límite se indetermina de la forma \displaystyle 1^\infty , es decir, por un lado queda

\displaystyle \lim_{x \to 1^{+}} \left(\frac{2x + 1}{x+2} \right)=1

y por otro lado

\displaystyle \lim_{x \to 1^{+}}\frac{1}{x-1}}=\infty

llegando a que la indeterminación es de la forma siguiente: \displaystyle 1^\infty

2 Para quitar esta indeterminación, a la base le sumamos y restamos \displaystyle 1 . Esto no altera el valor del límite, pues estamos sumando un cero.

\displaystyle \lim_{x \to 1^{+}} \left(\frac{2x + 1}{x+2} \right)^{\frac{1}{x-1}} = \lim_{x \to 1^{+}} \left( 1+\frac{2x + 1}{x+2} -1 \right)^{\frac{1}{x-1}}

3 Ponemos al mismo común denominador en los dos últimos sumandos  y reducimos la

expresión:

\displaystyle \lim_{x \to 1^{+}} \left( 1+\frac{2x + 1}{x+2} -\frac{x+2}{x+2} \right)^{\frac{1}{x-1}} =\lim_{x \to 1^{+}} \left(1 + \frac{x-1 }{x+2} \right)^{\frac{1}{x-1}}

recordando que

\displaystyle \frac{1}{\frac{a}{b}} = \frac{b}{a}

4 En el segundo, sumando, realizamos el inverso del inverso.

\displaystyle \lim_{x \to 1^{+}} \left(1 + \frac{1 }{\frac{x+2}{x-1}} \right)^{\frac{1}{x-1}}

5 Elevamos al denominador y a su inverso

\displaystyle \lim_{x \to 1^{+}} \left( \left( 1 + \frac{1 }{\frac{x+2}{x-1}} \right)^{\frac{1}{x-1}} \right)^{\frac{x-1}{x+2}\frac{x+2}{x-1}}

6 Si hacemos

\displaystyle c = \frac{x+2}{x-1}

,

recordando que

\displaystyle (a^b)^c = a^{bc}

y reducimos y reordenamos

\displaystyle \lim_{x \to 1^{+}} \left( \left( 1 + \frac{1 }{\frac{x+2}{x-1}} \right)^{\frac{x+2}{x-1}} \right)^{\frac{x-1}{x+2}\frac{1}{x-1}}=\lim_{x \to 1^{+}} \left( \left( 1 + \frac{1 }{c} \right)^{c} \right)^{\frac{1}{x+2}}

notamos que:

\displaystyle \lim_{x \to 1^{+}} c = \lim_{x \to 1^{+}} \frac{x+2}{x-1} = \infty

7 Usando la igualdad vista al inicio tendremos que

\displaystyle \lim_{x \to 1^{+}} e^{\frac{1}{x+2}} = e^{\frac{1}{3}}

Así, hemos logrado encontrar el límite deseado.

Segundo método de resolución de la indeterminación

En este segundo método usaremos la siguiente igualdad:

\displaystyle \lim_{x \to a} \left( \frac{f(x)}{g(x)}\right)^{h(x)} = e^{\lim_{x \to a} h(x) \left( \frac{f(x)}{g(x)} - 1 \right) }

1Notemos que el limite \displaystyle \lim_{x \to 1^{+}} \left( \frac{2x+1}{x+2} \right)^{\frac{1}{x-1}}  se indetermina de la forma \displaystyle 1^{\infty} .

2Usando la igualdad vista previamente con

\displaystyle f(x) = 2x+1
\displaystyle g(x) = x+2
\displaystyle h(x) = \frac{1}{x-1}

tenemos:

\displaystyle \lim_{x \to 1^{+}} \left( \frac{2x+1}{x+2} \right)^{\frac{1}{x-1}} = e^{\lim_{x\to 1^{+}} \frac{1}{x-1} \left( \frac{2x+1}{x+2} -1 \right)}

3Poniendo al mismo común denominador tenemos:

\displaystyle e^{\lim_{x\to 1^{+}} \frac{1}{x-1} \left( \frac{2x+1}{x+2} -\frac{x+2}{x+2} \right)}

4Resolvemos la resta en el exponente y así tenemos lo siguiente:

\displaystyle e^{\lim_{x \to 1^{+}} \frac{1}{x-1} \left( \frac{x-1}{x+2} \right)}

5Eliminado el factor común del numerador y denominador tendremos:

\displaystyle e^{\lim_{x\to 1^{+}} \left( \frac{1}{x+2} \right)}

6Así, resolviendo el límite en el exponente tenemos:

\displaystyle e^\frac{1}{3}

Con lo cual hemos sorteado la indeterminación.