FUNCIÓN CUADRÁTICA

Las funciones polinómicas son aquellas constituidas por un polinomio, un ejemplo de estas es la función cuadrática o de segundo grado, representada con una gráfica de parábola y la siguiente ecuación:

REPRESENTACIÓN GRÁFICA DE LA PARÁBOLA

Para construir una gráfica de parábola se requiere conocer los siguientes elementos:

VÉRTICE

Por el vértice pasa el eje de simetría de la parábola, es decir, cuando el coeficiente del término  es positivo el vértice será el punto más bajo de la gráfica y las fórmulas para encontrarlo son las siguiente:

Así mismo, la ecuación del eje de simetría es:

PUNTOS DE CORTE CON EL EJE X

Para encontrar el valor de  cuando , la segunda coordenada debe igualarse a cero, por lo que tendremos que resolver la siguiente igualdad:

Al resolver la ecuación anterior los resultados pueden ser:

1. Dos puntos de corte:  y  esto sucede si  0″>
2. Un punto de corte:  esto sucede si 
3. Ningún punto de corte si <img src=”https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-de1c6968f84eabe97541f252d18dbf5c_l3.png&#8221; alt=”b^{2}-4ac

PUNTO DE CORTE CON EL EJE Y

Para encontrar la intersección con el eje  la primera coordenada debe igualarse a cero, , por lo que tendremos:

EJEMPLO

Para representar la función  es necesario encontrar los siguientes elementos que componen la parábola:

VÉRTICE

Aplicamos las formulas descritas en el apartado anterior para encontrar la coordenadas del vértice que son:

Entonces las coordenadas del vértice son: 

PUNTOS DE CORTE CON EL EJE X

Para encontrar el punto o los puntos de corte con el eje X, igualamos la función con 0, tal como se indicó anteriormente:

Para resolver la ecuación, utilizamos la fórmula general para ecuaciones de segundo grado:

En este caso hemos encontrado dos puntos de corte los cuales son:  y 

PUNTO DE CORTE CON EL EJE Y

Para encontrar el punto de corte con  basta con conocer el valor de la constante  que en este caso es  y las coordenadas son: .

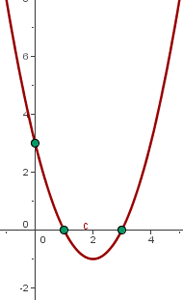
GRÁFICA DE LA FUNCIÓN CUADRÁTICA

Partimos de 

TRASLACIÓN VERTICAL

Si nuestra función es 

Donde:

• 0″>, entonces  se desplaza hacia arriba  unidades.
• <img src=”https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-54c02352ce9ea9031f39f5ecbc1227ab_l3.png&#8221; alt=”k, entonces  se desplaza hacia abajo  unidades.

En este caso el vértice de la parábola es: .

Y el eje de simetría .

TRASLACIÓN HORIZONTAL

Para la ecuación 

Donde:

• Si, 0″>, entonces  se desplaza hacia la izquierda  unidades.
• Si, <img src=”https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-2ebc041a93b1010f00e3dead8028115b_l3.png&#8221; alt=”h, entonces  se desplaza hacia la derecha  unidades.

En este ejercicio el vértice de la parábola es: .

Y el eje de simetría es .

TRASLACIÓN OBLICUA

Por último en la siguiente expresión ,el vértice de la parábola es: .

Y el eje de simetría es .