FRACCIONES

La fracción como partes de la unidad

El todo se toma como la unidad. La fracción expresa un valor con relación a ese todo.

La unidad fraccionaria es cada una de las partes que se obtienen al dividir la unidad en n partes iguales.

Entero dividido en cuartos y sextos representación gráfica

Ejemplo

Un depósito contiene $\cfrac{2}{3}$ de gasolina $Uso de las fracciones en el volumen de un recipiente representación gráfica$

El todo es el depósito.

La unidad equivale a $\cfrac{3}{3}$ , en este caso.

En general, el todo sería una fracción con el mismo número en el numerador y el denominador de la forma .

Ejemplo

$\cfrac{2}{3}$ de gasolina expresa la relación existente entre la gasolina y la capacidad del depósito. De sus tres partes dos están ocupadas por gasolina.

Concepto de fracción

Una fracción es el cociente de dos números enteros y , que representamos de la siguiente forma:

\cfrac{a}{b}\; \; \; \; \; \; \; \; \; \; b\neq 0

denominador , indica el número de partes en que se ha dividido la unidad.

numerador , indica el número de unidades fraccionarias elegidas.

Representación de fracciones

Cuartas partes de un entero representación gráfica

Sextas partes de un entero representación gráfica

La fracción como cociente

Repartir $4\: \euro$ entre cinco amigos: $\cfrac{4}{5}=0.8\: \euro$

La fracción como operador

Para calcular la fracción de un número, multiplicamos el numerador por el número y el resultado lo dividimos por el denominador.

Ejemplo

Calcular los $\cfrac{2}{3}$ de $60\: \euro$ :

La fracción como razón y proporción

Cuando comparamos dos cantidades de una magnitud, estamos usando las fracciones como razones.

Así, cuando decimos que la proporción entre chicos y chicas en el instituto es de a , estamos diciendo que por cada chicos hay chicas. Es decir, que de cada cinco estudiantes, son chicos y son chicas.

Porcentajes

Un caso particular de las fracciones como razón son los porcentajes, ya que estos no son más que la relación de proporcionalidad que se establece entre:

Un número y 100 tanto por ciento

Un número y 1000 tanto por mil

Un número y tanto por uno

Ejemplo

Luis compra una camisa por $35\: \euro$ , le hacen un descuento del $10\%$ . ¿Cuánto pagará por la camisa?

Tipos de fracciones

Fracciones propias

Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor está comprendido entre cero y uno.

Ejemplo:

{\displaystyle\frac{2}{3}, \frac{3}{5}, \frac{7}{10}}

Fracciones impropias

Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.

Ejemplo:

{\displaystyle\frac{5}{3}, \frac{7}{5}, \frac{13}{10}}

Número mixto

El número mixto o fracción mixta está compuesto de una parte entera y otra fraccionaria.

Para pasar de número mixto a fracción impropia:

1 Se deja el mismo denominador

2 El numerador se obtiene de la suma del producto del entero por el denominador más el numerador, del número mixto.

Ejemplo:

{3\displaystyle\frac{2}{5}=\frac{3(5)+2}{5}=\frac{17}{5}}

Para pasar una fracción impropia a número mixto:

1 Se divide el numerador por el denominador.

2 El cociente es el entero del número mixto.

3 El resto es el numerador de la fracción.

4 El denominador es el mismo que el de la fracción impropia.

Ejemplo:

{\displaystyle\frac{13}{5}=2\frac{3}{5}}

Fracciones decimales

Las fracciones decimales tienen como denominador una potencia de 10.

Ejemplo:

{\displaystyle\frac{23}{100}, \frac{12}{1000},\frac{3}{10}}

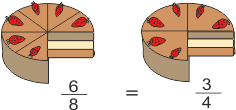
Fracciones equivalentes

Dos fracciones son equivalentes cuando el producto de extremos es igual al producto de medios

{\displaystyle\frac{a}{b}= \frac{c}{d} \ \ \ si \ \ \ ad=bc}

{a} y {d} son los extremos

{b} y {c} son los medios

Ejemplo:

Calcula si son equivalentes las fracciones ${\displaystyle\frac{4}{6}}$ y ${\displaystyle\frac{8}{12}}$

${4 \cdot 12 = 6 \cdot 8 = 48}$ entonces si son equivalentes.

Si se multiplica o divide el numerador y denominador de una fracción por un número entero, distinto de cero, se obtiene otra fracción equivalente a la dada.

Al primer caso le llamamos ampliar o amplificar.

Ejemplo:

{\displaystyle\frac{2}{3}=\frac{2(5)}{3(5)}=\frac{10}{15}}

Simplificar fracciones

Simplificar una fracción es transformarla en una fracción equivalente más simple.

1 Para simplificar una fracción dividimos numerador y denominador por un mismo número.

2 Empezaremos a simplificar probando por los primeros números primos: 2, 3, 5, 7, … Es decir, probamos a dividir numerador y denominador entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.

3 Se repite el proceso hasta que no haya más divisores comunes.

4 Si los términos de la fracción terminan en ceros, empezaremos quitando los ceros comunes finales del numerador y denominador, lo cual es equivalente a dividir numerador y denominador por la misma potencia de 10.

5 Si el número por el que dividimos es el máximo común divisor del numerador y denominador llegamos a una fracción irreducible que es equivalente a la inicial.

Ejemplo:

{\displaystyle\frac{8}{36}=\frac{8:4}{36:4}=\frac{2}{9}}

Fracciones irreducibles

Las fracciones irreducibles son aquellas que no se pueden simplificar, esto sucede cuando el numerador y el denominador son primos entre sí, o lo que es lo mismo, cuando el mcd de ambos números es 1.

Ejemplo:

{\displaystyle\frac{5}{7}, \ \frac{6}{13}, \ \frac{2}{5}}

Operaciones con fracciones

Suma y resta de fracciones

Con el mismo denominador

Se suman o se restan los numeradores y se mantiene el denominador.

\displaystyle \frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}

\displaystyle \frac{5}{7}+\frac{1}{7}=\frac{6}{7}

\displaystyle \frac{5}{7}-\frac{1}{7}=\frac{4}{7}

Con distinto denominador

En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.

Se determina el denominador común, que será el mínimo común múltiplo de los denominadores.

Este denominador, común, se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.

Se suman o se restan los numeradores de las fracciones equivalentes obtenidas.

\displaystyle \frac{a}{b}+\frac{c}{d}=\frac{a \cdot d + b \cdot c}{b \cdot d}

\displaystyle \frac{5}{4}+\frac{1}{6}=\frac{5 \cdot 3 + 1 \cdot 2}{12}=\frac{15 + 2}{12}=\frac{17}{12}

El m.c.m. de (4,6)=12 . Una manera fácil de encontrarlo es la siguiente:

Entonces podemos ver que para tener el mismo denominador, tenemos que multiplicar la primera fracción por , y la segunda por , lo que nos da $2 \cdot 2 \cdot 3=12$ .

\displaystyle \frac{5}{4}-\frac{1}{6}=\frac{5 \cdot 3 - 1 \cdot 2}{12}=\frac{15 - 2}{12}=\frac{13}{12}

Multiplicación de fracciones

La multiplicación de dos fracciones es otra fracción que tiene por numerador el producto de los numeradores y por denominador el producto de los denominadores.

\displaystyle \frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}

\displaystyle \frac{5}{4} \cdot \frac{1}{6}=\frac{5}{24}

Cociente de fracciones

La división de dos fracciones es otra fracción que tiene por numerador el producto de los extremos y por denominador el producto de los medios.

\displaystyle \frac{a}{b} \div \frac{c}{d}= \frac{a}{b} \cdot \frac{d}{c}= \frac{a \cdot d}{b \cdot c}

\displaystyle \frac{5}{7} \div \frac{1}{6}= \frac{5}{7} \cdot \frac{6}{1}= \frac{30}{7}

Operaciones combinadas y prioridades

1 Pasar a fracción los números mixtos y decimales.

2 Calcular las potencias y raíces.

3 Efectuar las operaciones entre paréntesis, corchetes y llaves.

4 Efectuar los productos y cocientes.

5 Realizar las sumas y restas.

Ejemplos de ejercicios y problemas con fracciones

1 $\displaystle \left [ \left ( 2 - 1\frac{3}{5} \right )^{2} + \left ( \frac{5}{8}-\frac{3}{4} \right )-\left ( \frac{6}{5} \cdot \frac{1}{3} \right )^{4} \cdot \left ( 7\frac{1}{2} \right )^{3}\right ] \div \left ( 5 - \frac{6}{5} \right )=$
Primero operamos con los productos y números mixtos dentro de los paréntesis.
$\displaystle \left [ \left ( 2 - \frac{8}{5} \right )^{2} + \left ( \frac{5}{8}-\frac{3}{4} \right )-\left ( \frac{6}{15} \right )^{4} \cdot \left ( \frac{15}{2} \right )^{3}\right ] \div \left ( 5 - \frac{6}{5} \right )=$
Luego, operamos en el primer paréntesis, quitamos el segundo, simplificamos en el tercero y operamos en el último.
$\displaystle \left [ \left ( \frac{2}{5} \right )^{2} + \left ( \frac{5}{8}-\frac{3}{4} \right )-\left ( \frac{2}{5} \right )^{4} \cdot \left ( \frac{15}{2} \right )^{3}\right ] \div \frac{19}{5}=$
Realizamos el producto y lo simplificamos.
$\displaystle \left ( \frac{4}{25} + \frac{5}{8}-\frac{3}{4} - \frac{16}{625} \cdot \frac{3375}{8}\right ) \div \frac{19}{5}=$
Cómo tenemos números muy grandes en la suma del primer paréntesis, operamos esta parte antes de seguir.
Tenemos:
$\displaystle \frac{16}{625} \cdot \frac{3375}{8}=$
Antes de hacer la suma, simplificamos.
$\displaystle \frac{16 \cdot 3375}{625 \cdot 8}= \frac{2 \cdot 3375}{625}=\frac{2 \cdot 27}{5}=\frac{54}{5}$
Realizamos las operaciones del paréntesis.
$\displaystle \left ( \frac{4}{25} + \frac{5}{8}-\frac{3}{4} - \frac{54}{5} \right ) \div \frac{19}{5}=$
Buscamos el mcm de 25, 8, 4, 5 , mirando cada número:
$25=5 \cdot 5$
$8=2 \cdot 2 \cdot 2$
$4=2 \cdot 2$
5=5
Nos damos cuenta que el m.c.m. es $5 \cdot 5 \cdot 2 \cdot 2 \cdot 2 =200$ .

Multiplicamos la primer fracción por $\displaystyle \frac{8}{8}$ , la segunda por $\displaystyle \frac{25}{25}$ , la tercera por $\displaystyle \frac{50}{50}$ y la cuarta por $\displaystyle \frac{40}{40}$ y obtenemos:

$\displaystle\left ( \frac{32}{200} + \frac{125}{200}-\frac{150}{200} - \frac{2160}{200} \right ) \div \frac{19}{5}=$

$\displaystle \frac{32+125-150-2160}{200} \div \frac{19}{5}=$

$\displaystle - \frac{2153}{200} \div \frac{19}{5}=$
Hacemos las operaciones y simplificamos el resultado.

$\displaystle - \frac{2153}{200} \cdot \frac{5}{19}= -\frac{10765}{3800}=-\frac{2153}{760}$

1 Una caja contiene bombones. Eva se comió $\displaystle \frac{1}{5}$
de los bombones y Ana $\displaystle \frac{1}{2}$ .

a ¿Cuántos bombones se comieron Eva, y Ana?

$\displaystyle \frac{1}{5} \cdot 60=\frac{60}{5}=12 \ \ \ \ \ \ \ \ \ \ \frac{1}{2} \cdot 60=\frac{60}{2}=30$
Eva se comió bombones y Ana .

b¿Qué fracción de bombones se comieron entre las dos

$\displaystyle \frac{1}{5} + \frac{1}{2}=$
El m.c.m. es .
Entonces multiplicamos la primera fracción por $\displaystyle \frac{2}{2}$ y la segunda por $\displaystyle \frac{5}{5}$ y obtenemos:
$\displaystyle \frac{1 \cdot 2}{5 \cdot 2} + \frac{1 \cdot 5}{2 \cdot 5}= \frac{2}{10}+ \frac{5}{10}=\frac{7}{10}$

3Un padre reparte entre sus hijos 1800 €. Al mayor le da $\displaystyle \frac{4}{9}$ de esa cantidad, al mediano $\displaystyle \frac{1}{3}$ y al menor el resto. ¿Qué cantidad recibió cada uno? ¿Qué fracción del dinero recibió el tercero?