Tasa de variación media
Consideremos una función  y consideremos dos puntos próximos sobre el eje de abscisas
y consideremos dos puntos próximos sobre el eje de abscisas  y
y  , siendo
, siendo  un número real que corresponde al incremento de
un número real que corresponde al incremento de  (
( ).
).
Se llama tasa de variación (TV) de la función en el intervalo ![\quad [a, a + h]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-d17b61a62c9fe71623dab02e1b1b9d6f_l3.png) , que se representa por
, que se representa por  , a la diferencia entre las ordenadas correspondientes a los puntos de las abscisas
, a la diferencia entre las ordenadas correspondientes a los puntos de las abscisas  y
y  .
.


TASA DE VARIACIÓN MEDIA
Se llama tasa de variación media (TVM) en intervalo ![\quad [a, a + h]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-d17b61a62c9fe71623dab02e1b1b9d6f_l3.png) , representada por
, representada por  o
o  , al cociente entre la tasa de variación y la amplitud del intervalo considerado sobre el eje de abscisas,
, al cociente entre la tasa de variación y la amplitud del intervalo considerado sobre el eje de abscisas,  o
o  , esto es:
, esto es:
![Rendered by QuickLaTeX.com \displaystyle \text{{\bf TVM}}[a, a + h] = \frac{f(a + h) - f(a)}{h}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-41efc118c1e74aecf222eb8dd14a9793_l3.png)
INTERPRETACIÓN GEOMÉTRICA
La expresión anterior coincide con la pendiente de la recta secante a la función  , que pasa por los puntos de abscisas
, que pasa por los puntos de abscisas  y
y  .
.

ya que en el triángulo  , de la imagen anterior, resulta que:
, de la imagen anterior, resulta que:

EJEMPLOS
1. Calcular la TVM de la función  en el intervalo
en el intervalo ![\quad [1, 4]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-db72c4b7329a74a430d14f0620f0eea0_l3.png) .
.
![Rendered by QuickLaTeX.com \begin{align*} \text{{\bf TVM}}[1, 4] &= \frac{f(4) - f(1)}{3}\\ &= \frac{12 - 0}{3}\\ &= 4 \end{align*}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-329dd8790c8512e9075304641c3667d7_l3.png)
2. El índice de la bolsa de Madrid pasó cierto año de  a
a  . Hallar la tasa de variación media mensual.
. Hallar la tasa de variación media mensual.

DERIVADA DE UNA FUNCIÓN EN UN PUNTO
La derivada de la función f(x) en el punto x = a es el valor del límite, si existe, de un cociente incremental cuando el incremento de la variable tiende a cero.


EJEMPLOS
1. Hallar la derivada de la función f(x) = 3x² en el punto x = 2.



2. Calcular la derivada de la función f(x) = x² + 4x − 5 en x = 1.




Interpretación geométrica de la derivada

Cuando  tiende a
tiende a  , el punto
, el punto  tiende a confundirse con el
tiende a confundirse con el  . Entonces la recta secante tiende a ser la recta tangente a la función
. Entonces la recta secante tiende a ser la recta tangente a la función  en
en  , y por tanto el ángulo
, y por tanto el ángulo  tiende a ser
tiende a ser  .
.


La pendiente de la tangente a la curva en un punto es igual a la derivada de la función en ese punto.

Ejemplo:
Dada la parábola  , hallar los puntos en los que la recta tangente es paralela a la bisectriz del primer cuadrante.
, hallar los puntos en los que la recta tangente es paralela a la bisectriz del primer cuadrante.
1 La bisectriz del primer cuadrante tiene como ecuación  , por tanto su pendiente es
, por tanto su pendiente es  .
.
2 Como las dos rectas son paralelas tendrán la misma pendiente, así que:
 .
.
3 Calculamos la pendiente de la tangente a la curva es igual a la derivada en el punto 

4 Igualamos ambas expresiones para la pendiente

5 Al resolver obtenemos la primera coordenada del punto

6 La segunda coordenada del punto la obtenemos sustituyendo el valor de  en la función
en la función 


Interpretación física de la derivada
VELOCIDAD MEDIA
La velocidad media es el cociente entre el espacio recorrido (Δe) y el tiempo transcurrido (Δt).


VELOCIDAD INSTANTÁNEA


EJEMPLO
La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es e(t) = 6t². Calcular:
1. la velocidad media entre t = 1 y t = 4.
La velocidad media es el cociente incremental en el intervalo [1, 4].

2. La velocidad instantánea en t = 1.
La velocidad instantánea es la derivada en t = 1.



DEFINICIÓN DE DERIVADA
Existen varias formas de definir la derivada, estás tienen que ver con geometría, física, economía, pero al final todas son la misma.
Desde el punto de vista geométrico, la derivada representa la pendiente de la recta tangente a la gráfica de la función. La derivada de una función  viene dada por
viene dada por

Se dice que la derivada de  existe si el límite existe; en caso de que el límite no exista, se dice que la derivada no existe.
existe si el límite existe; en caso de que el límite no exista, se dice que la derivada no existe.
EJERCICIO DE DERIVADA DE UNA FUNCIÓN LINEAL
1Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

EJERCICIOS DE DERIVADAS DE FUNCIONES CUADRÁTICAS
2Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

3Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

EJERCICIOS DE DERIVADAS DE FUNCIONES CÚBICAS
4Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

5Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

EJERCICIO DE DERIVADAS DE COCIENTES
6Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

7Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y simplificamos
![Rendered by QuickLaTeX.com {\begin{array}{rcl} \displaystyle \frac{f(x+h) - f(x)}{h} & = & \displaystyle \frac{\displaystyle \frac{x^2 + 2xh + h^2 + 1}{(x + h)^2 - 1} - \displaystyle \frac{x^2 + 1}{x^2 - 1}}{h} \\\\ & = & \displaystyle \frac{\displaystyle \frac{(x^2 + 2xh + h^2 + 1)(x^2 - 1)-(x^2 + 1)(x^2 + 2xh + h^2 - 1)}{(x^2 - 1)[(x + h)^2 - 1]}}{h} \\\\ & = & \displaystyle \frac{\displaystyle \frac{-4xh - 2h^2}{(x^2 - 1)[(x + h)^2 - 1]}}{h} \\\\ & = & \displaystyle \frac{-h(4x + 2h)}{h(x^2 - 1)[(x + h)^2 - 1]} \\\\ & = & \displaystyle \frac{-(4x + 2h)}{(x^2 - 1)[(x + h)^2 - 1]} \end{array}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-cfa2229c6ae98bd8b9891fa1a5293cdd_l3.png)
3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior
![Rendered by QuickLaTeX.com {\begin{array}{rcl} f'(x) & = & \displaystyle \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\\\ & = & \displaystyle \lim_{h \to 0} \displaystyle \frac{-(4x + 2h)}{(x^2 - 1)[(x + h)^2 - 1]} \\\\ & = & -\displaystyle \frac{4x}{(x^2 - 1)^2} \end{array}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-934145c040bee23c4b30c65dca9891cf_l3.png)
EJERCICIOS DE DERIVADAS DE RAÍCES
8Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y racionalizamos para tratar con el denominador 

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

9Encontrar la derivada mediante límites de 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada y racionalizamos para tratar con el denominador 
![Rendered by QuickLaTeX.com {\begin{array}{rcl} \displaystyle \frac{f(x+h) - f(x)}{h} & = & \displaystyle \frac{\displaystyle \frac{5}{\sqrt{3x + 3h - 1}} - \displaystyle \frac{5}{\sqrt{3x - 1}}}{h} \\\\ & = & \displaystyle \frac{5(\sqrt{3x - 1} - \sqrt{3x + 3h - 1})}{h(\sqrt{3x - 1})(\sqrt{3x + 3h - 1})} \\\\ & = & \displaystyle \frac{5(\sqrt{3x - 1} - \sqrt{3x + 3h - 1})}{h(\sqrt{3x - 1})(\sqrt{3x + 3h - 1})} \cdot \displaystyle \frac{\displaystyle \sqrt{3x - 1} + \displaystyle \sqrt{3x + 3h - 1}}{\displaystyle \sqrt{3x - 1} + \displaystyle \sqrt{3x + 3h - 1}} \\\\ & = & \displaystyle \frac{5[(3x - 1) - (3x + 3h - 1)]}{h(\sqrt{3x - 1})(\sqrt{3x + 3h - 1})\left( \displaystyle \sqrt{3x - 1} + \displaystyle \sqrt{3x + 3h - 1} \right)} \\\\ & = & \displaystyle \frac{5(-3h)}{h(\sqrt{3x - 1})(\sqrt{3x + 3h - 1})\left( \displaystyle \sqrt{3x - 1} + \displaystyle \sqrt{3x + 3h - 1} \right)} \\\\ & = & \displaystyle \frac{-15}{(\sqrt{3x - 1})(\sqrt{3x + 3h - 1})(\displaystyle \sqrt{3x - 1} + \displaystyle \sqrt{3x + 3h - 1})} \end{array}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-984dc0e38147c9335f8628945f535ffb_l3.png)
3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior
tiende a cero al cociente anterior

EJERCICIO DONDE NO EXISTE LA DERIVADA
10Encontrar la derivada mediante límites de  en
en 
Solución
1Encontramos 

2Calculamos el cociente de la definición de derivada

3La derivada resulta de calcular el límite cuando  tiende a cero al cociente anterior en
tiende a cero al cociente anterior en 

4La función valor absoluto se expresa de la forma
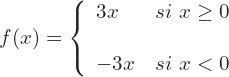
Así, los límites laterales para  no son iguales
no son iguales

y por tanto la derivada de  en
en  no existe
no existe
Derivadas laterales
DERIVADA POR LA IZQUIERDA

DERIVADA POR LA DERECHA

Una función es derivable en un punto si, y sólo si, es derivable por la izquierda y por la derecha en dicho punto y las derivadas laterales coinciden.
DERIVADA DE LAS FUNCIONES A TROZOS
En las funciones definidas a trozos es necesario estudiar las derivadas laterales en los puntos de separación de los distintos trozos.
Ejemplos
Estudiar la derivabilidad de la función f(x) = |x|.



Puesto que las derivadas laterales en x = 0 son distintas, la función no es derivable en dicho punto.

Las derivada laterales no coinciden en los picos ni en los puntos angulosos de las funciones. Por tanto en esos puntos no existe la derivada.
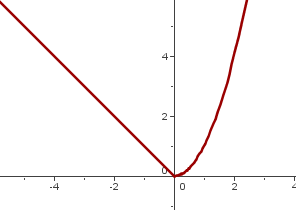
Estudiar la derivabilidad de la función:



No es derivable en x = 0.
Derivabilidad y continuidad
Si una función es derivable en un punto x = a, entonces es continua para x = a.
El reciproco es falso, es decir, hay funciones que son continuas en un punto y que, sin embargo, no son derivables.
Ejemplos
Estudiar la continuidad y derivabilidad de las funciones:
1. 
En primer lugar estudiamos la continuidad en x = 0.

La función no es continua, por tanto tampoco es derivable.

2. 
En primer lugar estudiamos la continuidad en x = 0.

La función es continua, por tanto podemos estudiar la derivabilidad.


Como no coinciden las derivadas laterales no es derivable en x = 0.

3. f(x) = x² en x = 0.
La función es continua en x = 0, por tanto podemos estudiar la derivabilidad.

En x = 0 la función es continua y derivable.
