PROGRAMACIÓN LINEAL

La programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.

Su empleo es frecuente en aplicaciones de la industria, la economía, la estrategia militar, etc.

Función objetivo

En esencia la programación lineal consiste en optimizar (maximizar o minimizar) una función objetivo, que es una función lineal de varias variables:

Restricciones

La función objetivo está sujeta a una serie de restricciones, expresadas por inecuaciones lineales:

Intersección entre dos rectas para programación lineal representacion grafica

Cada desigualdad del sistema de restricciones determina un semiplano.

Semiplano formado por las soluciones de dos desigualdades en programación lineal representacion grafica

Solución factible

El conjunto intersección, de todos los semiplanos formados por las restricciones, determina un recinto, acotado o no, que recibe el nombre de región de validez o zona de soluciones factibles.

Región de validez entre dos rectas en programación lineal representacion grafica

Solución óptima

El conjunto de los vértices del recinto se denomina conjunto de soluciones factibles básicas y el vértice donde se presenta la solución óptima se llama solución máxima (o mínima según el caso).

Valor del programa lineal

El valor que toma la función objetivo en el vértice de solución óptima se llama valor del programa lineal.

Pasos para resolver un problema de programación lineal

1 Elegir las incógnitas.

2 Escribir la función objetivo en función de los datos del problema.

3 Escribir las restricciones en forma de sistema de inecuaciones.

4 Averiguar el conjunto de soluciones factibles representando gráficamente las restricciones.

5 Calcular las coordenadas de los vértices del recinto de soluciones factibles (si son pocos).

6 Calcular el valor de la función objetivo en cada uno de los vértices para ver en cuál de ellos presenta el valor máximo o mínimo según nos pida el problema (hay que tener en cuenta aquí la posible no existencia de solución si el recinto no está acotado).

Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas. El fabricante dispone para la confección de 750 m de tejido de algodón y 1000 m de tejido de poliéster. Cada pantalón precisa 1 m de algodón y 2 m de poliéster. Para cada chaqueta se necesitan 1.5 m de algodón y 1 m de poliéster. El precio del pantalón se fija en 50 € y el de la chaqueta en 40 €.

¿Qué número de pantalones y chaquetas debe suministrar el fabricante a los almacenes para que estos consigan una beneficio máxima?

Solución:

1 Elección de las incógnitas

2 Función objetivo

3 Restricciones

Para escribir las restricciones vamos a ayudarnos de una tabla:

Como el número de pantalones y chaquetas son números naturales, tendremos dos restricciones más:

4 Hallar el conjunto de soluciones factibles

Tenemos que representar gráficamente las restricciones.

Al ser ${x \ge 0}$ e ${y \ge 0}$ , trabajaremos en el primer cuadrante.

Representamos las rectas, a partir de sus puntos de corte con los ejes.

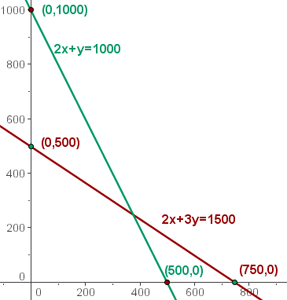
Ejercicio de programacion lineal 1 representación gráfica

Resolvemos gráficamente la inecuación: ${x + 1.5y \le 750}$ , para ello tomamos un punto del plano, por ejemplo el {(0,0)} .

${0 \le 750}$ entonces el punto {(0,0)} se encuentra en el semiplano donde se cumple la desigualdad.

De modo análogo resolvemos ${2x + y \le 1000}$ .

La zona de intersección de las soluciones de las inecuaciones sería la solución al sistema de inecuaciones, que constituye el conjunto de las soluciones factibles.

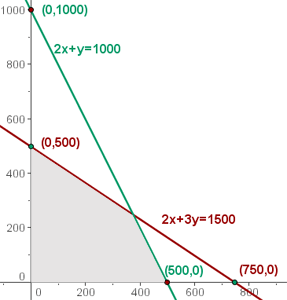
representación gráfica en Ejercicio de programacion lineal

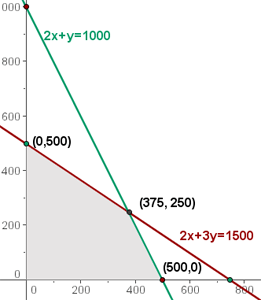
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

La solución óptima, si es única, se encuentra en un vértice del recinto. Estas son las soluciones a los sistemas:

{2x + 3y = 1500; \ \ \ x = 0; \ \ \ \Longrightarrow \ \ \ (0, 500)}

{2x + y = 1000; \ \ \ y = 0; \ \ \ \Longrightarrow \ \ \ (500, 0)}

{2x + 3y =1500; \ \ \ 2x + y = 1000; \ \ \ \Longrightarrow \ \ \ (375, 250)}

Ejercicio de programacion lineal representación gráfica

6 Calcular el valor de la función objetivo

En la función objetivo sustituimos cada uno de los vértices.

{f(0, 500) = 50(0) + 40(500) = 20 000} €

{f(500, 0) = 50(500) + 40(0) = 25 000} €

{f(375, 250) = 50(375) + 40(250) = 28 750} € entonces es un Máximo

La solución óptima es fabricar 375 pantalones y 250 chaquetas para obtener un beneficio de 28750 €.

Solución múltiple

La solución no siempre es única, también podemos encontrarnos con una solución múltiple.

Si la función objetivo del ejercicio anterior hubiese sido:

{f(0,500) = 20(0) + 30(500) = 15 000} € entonces es un Máximo

{f(500, 0) = 20(500) + 30(0) = 10 000} €

{f(375, 250) = 20(375) + 30(250) = 15 000} € entonces es un Máximo

En este caso todos los pares, con soluciones enteras, del segmento trazado en negro serían máximos.

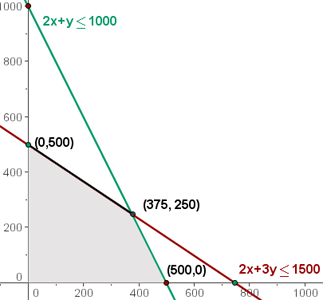
Ejercicio de programación lineal 4 representación gráfica

{f(300, 300)= 20(300) + 30(300) = 15 000} € Máximo

	$a_{1}x+b_{1}y\leq c_{1}$
$a_{2}x+b_{2}y\leq c_{2}$
… … …
$a_{n}x+b_{n}y\leq c_{n}$