- Para representar los puntos en el plano, necesitamos dos rectas perpendiculares, llamados ejes cartesianos o ejes de coordenadas.
- El punto
 , donde se cortan los dos ejes, es el origen de coordenadas
, donde se cortan los dos ejes, es el origen de coordenadas  .
. - El eje horizontal se llama eje
 o eje de abscisas.
o eje de abscisas. - La coordenada
 es positiva a la derecha del origen.
es positiva a la derecha del origen. - La coordenada
 es negativa a la izquierda del origen.
es negativa a la izquierda del origen. - El eje vertical se llama eje
 o eje de ordenadas.
o eje de ordenadas. - La coordenada
 es positiva por encima del origen.
es positiva por encima del origen. - La coordenada
 es negativa por debajo del origen.
es negativa por debajo del origen. - Las coordenadas de un punto cualquiera
 se representan por
se representan por  .
. - La primera coordenada se mide sobre el eje de abscisas, y se la denomina coordenada
 del punto o abscisa del punto.
del punto o abscisa del punto. - La segunda coordenada se mide sobre el eje de ordenadas, y se le llama coordenada
 del punto u ordenada del punto.
del punto u ordenada del punto.

Representación de puntos
Vamos a representar en unos ejes de coordenadas el punto P(2, 4):
1Marcamos la primera coordenada (la absisa) en el eje OX y la segunda coordenada (la ordenada) en el eje OY
2Desde cada punto trazamos una recta discontinua paralela al otro punto y el punto de corte entre las dos rectas es el punto buscado.


Representación de puntos
Vamos a representar en unos ejes de coordenadas el punto P(2, 4):
1Marcamos la primera coordenada (la absisa) en el eje OX y la segunda coordenada (la ordenada) en el eje OY
2Desde cada punto trazamos una recta discontinua paralela al otro punto y el punto de corte entre las dos rectas es el punto buscado.


Signos de cada cuadrante

| Abscisa | Ordenada | |
|---|---|---|
| 1er cuadrante | + | + |
| 2º cuadrante | − | + |
| 3er cuadrante | − | − |
| 4º cuadrante | + | − |
El origen de coordenadas, O, tiene de coordenadas: O(0, 0).

Los puntos que están en el eje de ordenadas tienen su abscisa igual a 0.

Los puntos situados en el eje de abscisas tienen su ordenada igual a 0.

Los puntos situados en la misma línea horizontal (paralela al eje de abscisas) tienen la misma ordenada.

Los puntos situados en una misma línea vertical (paralela al eje de ordenadas) tienen la misma abscisa.

Ejemplos
Representa en los ejes de coordenadas los puntos:
A(1, 4), B(–3, 2), C(0, 5), D(–4, –4), E(–5, 0), F(4, –3), G(0, –2), I(3, 0),

Una tabla de valores es una representación de datos, mediante pares ordenados, que expresan la relación existente entre dos magnitudes o dos situaciones.
La siguiente tabla nos muestra la variación del precio de las patatas, según el número de kilogramos que compremos.
| Kg de patatas | Precio en € |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
La siguiente tabla nos indica el número de alumnos que consiguen una determinada nota en un examen.
| Nota | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nº de alumnos | 1 | 1 | 2 | 3 | 6 | 11 | 12 | 7 | 4 | 2 | 1 |
Las tablas de valores se utilizan para representar estos valores en unos ejes de coordenada teniendo en cuenta que la primera columna o fila (dependiendo de la orientación que le demos) es la de la coordenada x y la segunda de la coordena y.
Representamos los valores de la primera tabla en unos ejes de coordenadas:

Si unimos estos puntos obtenemos una gráfica

A medida que compramos más patatas el precio de esta va aumentando proporcionalmente
Todo sobre la representación gráfica
- Una gráfica es la representación en unos ejes de coordenadas de los pares ordenados de una tabla.
- La variable que se representa en el eje horizontal se llama variable independiente o variable
 .
. - La variable que se representa en el eje vertical se llama variable dependiente o variable
 .
. - La variable
 está en función de la variable
está en función de la variable  .
. - Las gráficas describen relaciones entre dos variables.
- Una vez realizada la gráfica podemos estudiarla, analizarla y extraer conclusiones.
- Para interpretar una gráfica, hemos de observarla de izquierda a derecha.
- El segundo paso es analizar cómo varía la variable dependiente
 , al aumentar la variable independiente
, al aumentar la variable independiente  .
.
Ejemplos de representaciones gráficas
1 La siguiente tabla dos muestra la variación del precio de las patatas, según el número de kilogramos que compremos.
| Kg de patatas | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Precio en € | 2 | 4 | 6 | 8 | 10 |

En esa gráfica podemos observar que a medida que compramos más kilos de patatas el precio se va incrementando.
2 La siguiente tabla nos indica el número de alumnos que consiguen una determinada nota en un examen.
| Nota | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nº de alumnos | 1 | 1 | 2 | 3 | 6 | 11 | 12 | 7 | 4 | 2 | 1 |
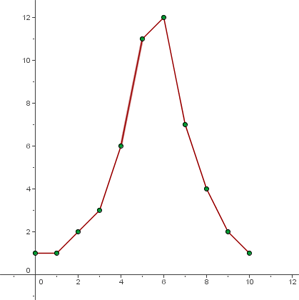
En esta gráfica observamos que la mayor parte de los alumnos obtienen una nota comprendida entre 4 y 7.
TIPOS DE GRÁFICAS
Gráfica creciente
Una gráfica es creciente si al aumentar la variable independiente aumenta la variable dependiente.

Gráfica decreciente
Una gráfica es decreciente si al aumentar la variable independiente disminuye la variable dependiente.
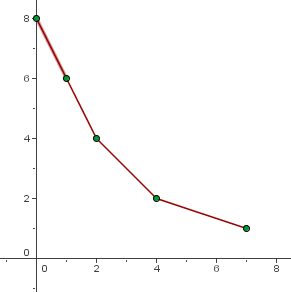
Una gráfica puede tener a la vez partes crecientes y decrecientes.

Gráfica constante
Una gráfica es constante si al variar la variable independiente la variable dependiente permanece invariable.

Concepto de función
Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda, llamada imagen.
Ejemplo:
El precio de un viaje en taxi viene dado por:
y = 0.5x + 3
Siendo x el tiempo en minutos que dura el viaje.
Como podemos observar, la función relaciona dos variables. x e y.
x es la variable independiente.
y es la variable dependiente (depende de los minutos que dure el viaje).
Las funciones se representan sobre unos ejes cartesianos para estudiar mejor su comportamiento.
| x | 0 | 10 | 20 | 30 |
|---|---|---|---|---|
| y = 0.5x + 3 | 3 | 8 | 13 | 18 |
Hemos hallado la variable dependiente (y), sustituyendo los valores de la variable independiente (x) en la función.
y = 0.5 · 0 + 3 = 3
y = 0.5 ·10 + 3 = 8
y = 0.5 · 20 + 3 = 13
y = 0.5 · 30 + 3 = 18

Función lineal y función identidad
La función lineal es del tipo:
y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.
Para su representación son necesarios al menos dos puntos.
Ejemplo:
y = 2x
Le damos valores a la función
y = 2 · 0 = 0
y = 2 · 1 = 2
y = 2 · 2 = 4
y = 2 · 3 = 6
y = 2 · 4 = 8
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y = 2x | 0 | 2 | 4 | 6 | 8 |

Pendiente
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.

Función identidad
La función identidad es del tipo:
y = x
Su gráfica es una recta que:
Pasa por el origen de coordenadas
Tiene de pendiente: m = 1
Forma con la parte positiva del eje de abscisas un ángulo de 45º

Función constante
La función constante es del tipo:
y = n
El criterio viene dado por un número real.
La pendiente es 0.
La gráfica es una recta horizontal paralela a al eje de abscisas.
Ejemplo:
Representar la función y = 3
Para representar la función trazamos una recta paralela al eje de abscisas que pase por (0, 3)
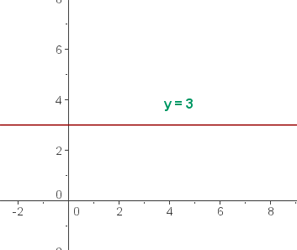
La gráfica es una recta vertical paralela a al eje de abscisas.
Las rectas paralelas al eje de ordenadas no son funciones, ya que un valor de x tiene infinitas imágenes y para que sea función sólo puede tener una. Son del tipo:
x = K

Funciones II

Las funciones algebraicas
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas
Si se pueden obtener las imágenes de  por simple sustitución como en este ejemplo :
por simple sustitución como en este ejemplo : 
Funciones implícitas
Si no se pueden obtener las imágenes de  por simple sustitución, sino que es necesario efectuar operaciones, como en este ejemplo
por simple sustitución, sino que es necesario efectuar operaciones, como en este ejemplo 
Ademas de esta clasificación, hay 6 otros tipos de funciones algebraicas
1 Funciones polinómicas
- Son las funciones que vienen definidas por un polinomio.

- Su dominio es
 , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.
2 Funciones constantes
- El criterio viene dado por un número real.

- La gráfica es una recta horizontal paralela a al eje de abscisas.
3 Funciones polinomicas de primer grado
1
- Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
- Son funciones de este tipo las siguientes:
- Función afín
2 
- Función lineal
3 
- Función identidad
4 
- Funciones cuadráticas
- Son funciones polinómicas de segundo grado,
- La gráfica de una función polinómica es una parábola.
4 Funciones racionales

- El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
- El criterio viene dado por un cociente entre polinomios:
5 Funciones radicales
- El criterio viene dado por la variable x bajo el signo radical.
- El dominio de una función irracional de índice impar es
 .
. - El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
6 Funciones algebraicas a trozos
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Funciones en valor absoluto
Función parte entera de x
Función mantisa
Función signo
Las funciones trascendentes
La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
1 Funciones exponenciales

Sea a un número real positivo. La función que a cada número real  le hace corresponder la potencia
le hace corresponder la potencia  se llama función exponencial de base
se llama función exponencial de base  y exponente
y exponente  .
.
2 Funciones logarítmicas
La función logarítmica en base a es la función inversa de la exponencial
en base a.


3 Funciones trigonométricas
Función seno

Función coseno

Función tangente

Función cosecante

Función secante

Función cotangente

Función cuadrática
Las funciones polinómicas son aquellas constituidas por un polinomio, un ejemplo de estas es la función cuadrática o de segundo grado, representada con una gráfica de parábola y la siguiente ecuación:

Representación gráfica de la parábola
Para construir una gráfica de parábola se requiere conocer los siguientes elementos:
Vértice
Por el vértice pasa el eje de simetría de la parábola, es decir, cuando el coeficiente del término  es positivo el vértice será el punto más bajo de la gráfica y las fórmulas para encontrarlo son las siguiente:
es positivo el vértice será el punto más bajo de la gráfica y las fórmulas para encontrarlo son las siguiente:


Así mismo, la ecuación del eje de simetría es:

Puntos de corte con el eje X
Para encontrar el valor de  cuando
cuando  , la segunda coordenada debe igualarse a cero, por lo que tendremos que resolver la siguiente igualdad:
, la segunda coordenada debe igualarse a cero, por lo que tendremos que resolver la siguiente igualdad:

Al resolver la ecuación anterior los resultados pueden ser:
- Dos puntos de corte:
 y
y  esto sucede si
esto sucede si 
- Un punto de corte:
 esto sucede si
esto sucede si 
- Ningún punto de corte si b2 -4ac< 0
Punto de corte con el eje Y
Para encontrar la intersección con el eje  la primera coordenada debe igualarse a cero,
la primera coordenada debe igualarse a cero,  , por lo que tendremos:
, por lo que tendremos:

Ejemplo
Para representar la función  es necesario encontrar los siguientes elementos que componen la parábola:
es necesario encontrar los siguientes elementos que componen la parábola:
Vértice
Aplicamos las formulas descritas en el apartado anterior para encontrar la coordenadas del vértice que son:


Entonces las coordenadas del vértice son: 
Puntos de corte con el eje X
Para encontrar el punto o los puntos de corte con el eje X, igualamos la función con 0, tal como se indicó anteriormente:

Para resolver la ecuación, utilizamos la fórmula general para ecuaciones de segundo grado:


En este caso hemos encontrado dos puntos de corte los cuales son:  y
y 
Punto de corte con el eje Y
Para encontrar el punto de corte con  basta con conocer el valor de la constante
basta con conocer el valor de la constante  que en este caso es
que en este caso es  y las coordenadas son:
y las coordenadas son:  .
.
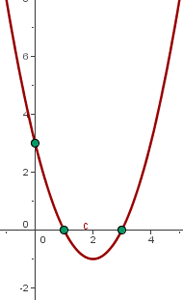
Gráfica de la función cuadrática
Partimos de 


Traslación vertical
Si nuestra función es 
Donde:
 , entonces
, entonces  se desplaza hacia arriba
se desplaza hacia arriba  unidades.
unidades.- k < 0, entonces
 se desplaza hacia abajo
se desplaza hacia abajo  unidades.
unidades.
En este caso el vértice de la parábola es:  .
.
Y el eje de simetría  .
.

Traslación horizontal
Para la ecuación 
Donde:
- Si,
 , entonces
, entonces  se desplaza hacia la izquierda
se desplaza hacia la izquierda  unidades.
unidades. - Si, h < 0, entonces
 se desplaza hacia la derecha
se desplaza hacia la derecha  unidades.
unidades.
En este ejercicio el vértice de la parábola es:  .
.
Y el eje de simetría es  .
.

Traslación oblicua
Por último en la siguiente expresión  ,el vértice de la parábola es:
,el vértice de la parábola es:  .
.
Y el eje de simetría es  .
.

Traslaciones de parábolas
Partimos de y = x²
| x | y = x² |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |

Caso 1: Traslación vertical
y = x² + k
Si k > 0, y = x² se desplaza hacia arriba k unidades
Si k < 0, y = x² se desplaza hacia abajo k unidades
El vértice de la parábola es: (0, k)
El eje de simetría x = 0


y = x² + 2 y = x² − 2
Caso 2: Traslación horizontal
y = (x + h)²
Si h > 0, y = x² se desplaza hacia la izquierda h unidades
Si h < 0, y = x² se desplaza hacia la derecha h unidades
El vértice de la parábola es: (−h, 0)
El eje de simetría es x = −h


y = (x + 2)²y = (x − 2)²
Caso 3: Traslación oblicua
y = (x + h)² + k
El vértice de la parábola es: (−h, k)
El eje de simetría es x = −h


y = (x − 2)² + 2 y = (x + 2)² − 2
Dilataciones y contracciones de funciones
Contracción de una función
Una función f(k·x) se contrae si K > 1.

Dilatación de una función
Una función f(k·x) se dilata si 0 < K < 1.

Funciones racionales
El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de  que anulan el denominador.
que anulan el denominador.
Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:


Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones


Traslaciones de hipérbolas
Las hipérbolas  son las más sencillas de representar.
son las más sencillas de representar.
Sus asítontas son los ejes
El centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen

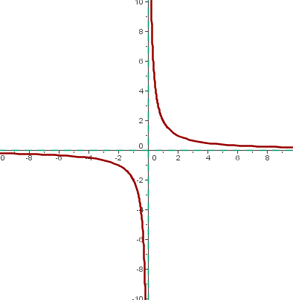
A partir de estas hipérbolas se obtienen otras por traslación.
Caso 1: Traslación vertical

El centro de la hipérbola es: (0, a)
Si a > 0,  se desplaza hacia arriba a unidades
se desplaza hacia arriba a unidades


El centro de la hipérbola es: (0, 3)
Si a < 0,  se desplaza hacia abajo a unidades
se desplaza hacia abajo a unidades


Caso 2: Traslación horizontal

El centro de la hipérbola es: (–b, 0)
Si< b > 0,  se desplaza a la izquierda b unidades
se desplaza a la izquierda b unidades


El centro de la hipérbola es: (-3, 0)
Si b < 0,  se desplaza a la derecha b unidades
se desplaza a la derecha b unidades


El centro de la hipérbola es: (3, 0)
Caso 3: Traslación oblicua

El centro de la hipérbola es: (–b, a)


El centro de la hipérbola es: (3, 4).
Para representar hipérbolas del tipo:

se divide y se escribe como:

Su representación gráfica es una hipérbola de centro (–b, a) y de asíntotas paralelas a los ejes.
Ejemplo




El centro de la hipérbola es: (-1, 3).
Dominio de las funciones radicales
El criterio de las funciones radicales viene dado por la variable  bajo el signo radical.
bajo el signo radical.
Función radical de índice impar
Estas funciones tienen como dominio los números reales 
Ejemplos de funciones radicales de índice impar
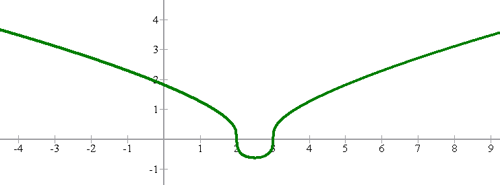
1![{f(x)=\sqrt[3]{x^{2}-5x+6}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-6c3dbd2d1e35574caf608eeab8ed9170_l3.png)
1Como el índice radical de  es impar, entonces el dominio de
es impar, entonces el dominio de  son todos los números reales
son todos los números reales  .
.
2Su gráfica es
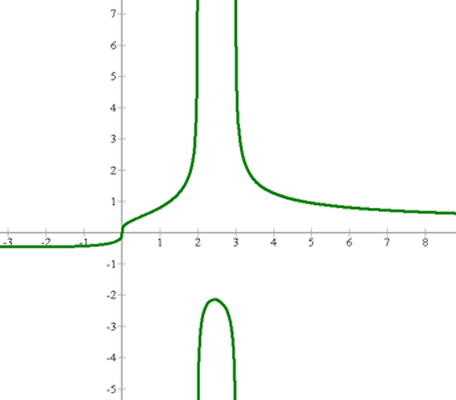
2![{f(x)=\sqrt[3]{\displaystyle\frac{x}{x^{2}-5x+6}}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-fdd09e3d8945da2266bdcf94b881d7ed_l3.png)
1Como el índice radical de  es impar, entonces su dominio de
es impar, entonces su dominio de  debería ser todos los números reales
debería ser todos los números reales  , pero al mismo tiempo posee un denominador que se hace cero cuando
, pero al mismo tiempo posee un denominador que se hace cero cuando  .
.
2Combinando ambas informaciones, el dominio de  es
es

3Su gráfica es
Función radical de índice par
El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Ejemplos de funciones radicales de índice par
1
1Para calcular el dominio hacemos el radicando mayor o igual que cero

2Notamos que para  se satisface la desigualdad.
se satisface la desigualdad.
3Los valores  dividen la recta real en tres intervalos:
dividen la recta real en tres intervalos: ![{(-\infty, 2], [2,3]}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-7026d8f28887e5c3d91d827e13caafb9_l3.png) y
y 
4Verificamos cuales de los tres intervalos satisfacen la desigualdad, los que satisfagan conformarán el dominio
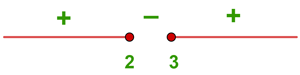
5El dominio de  es
es ![{(-\infty, 2] \cup [3,\infty)}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-65bd3b73669122504b8ddd8873eae009_l3.png)
6La gráfica de  es
es
2
1Para calcular el dominio hacemos el radicando mayor o igual que cero

2El dominio del radicando es ![{(-\infty, 2] \cup [3,\infty)}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-65bd3b73669122504b8ddd8873eae009_l3.png)
3Eldenominador de  se hace cero cuando
se hace cero cuando  , por ello no puede ser parte del dominio.
, por ello no puede ser parte del dominio.
4El dominio de  es
es ![{(-\infty,-4)\cup (-4, 2] \cup [3,\infty)}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-1ca4c19f6805fdf43af2d1a1b0924d26_l3.png)
5La gráfica de  es
es

3
1Para calcular el dominio hacemos el radicando mayor que cero, no puede ser igual a cero ya que se encuentra en el denominador

2El dominio de  es
es 
5La gráfica de  es
es

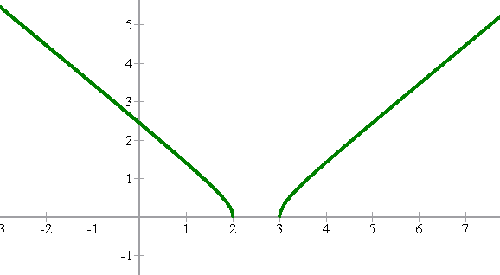
4
1Para calcular el dominio hacemos el radicando mayor o igual que cero

2Notamos que para  hacen cero el denominador, mientras que
hacen cero el denominador, mientras que  satisface la desigualdad.
satisface la desigualdad.
3Los valores anteriores dividen la recta real en cuatro intervalos: ![{(-\infty, -4), (-4,2], [2,3]}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-df750ae4c43ee25944a57be8119c5ecc_l3.png) y
y 
4Verificamos cuales de los cuatro intervalos satisfacen la desigualdad, los que satisfagan conformarán el dominio

5El dominio de  es
es 
6La gráfica de  es
es

Funciones definidas a trozos
Son funciones definidas por distintos criterios, según los intervalos que se consideren.

El dominio lo forman todos los números reales menos el 2.
Función parte entera de x
Es una función que a cada número real hace corresponder el número entero inmediatamente inferior.
f(x) = E(x)
xf(x) = E(x)
| 0 | 0 |
| 0.5 | 0 |
| 0.9 | 0 |
| 1 | 1 |
| 1.5 | 1 |
| 1.9 | 1 |
| 2 | 2 |

Función mantisa
Función que hace corresponder a cada número el mismo número menos su parte entera.
f(x) = x – E(x)
xf(x) = x – E(x)
| 0 | 0 |
| 0.5 | 0.5 |
| 0.9 | 0.9 |
| 1 | 0 |
| 1.5 | 0.5 |
| 1.9 | 0.9 |
| 2 | 0 |

Función signo
f(x) = sgn(x)


Función valor absoluto
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces
2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo
3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función
4. Representamos la función resultante
Ejemplos
1. 
Igualamos a cero la función, sin el valor absoluto, y se calculan sus raíces

Se forman intervalos con la raíz y se evalúa el signo de cada intervalo

Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función

Representamos la función

D = ℛ
2. 
Igualamos a cero la función, sin el valor absoluto, y se calculan sus raíces

Se forman intervalos con la raíces y se evalúa el signo de cada intervalo

Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función

Representamos la función

D = ℛ
La función exponencial
La función exponencial es aquella que a cada valor real  le asigna la potencia
le asigna la potencia  con
con  0}»> y
0}»> y  . Esta función se expresa
. Esta función se expresa

el número  se denomina base.
se denomina base.
Gráficas de funciones exponenciales
Estudiemos el comportamiento de la función exponencial de acuerdo a su base
Construimos una tabla de valores para 
 |  |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Trazamos la gráfica

Ahora construimos una tabla de valores para 
 |  |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
Trazamos la gráfica

Observamos que la primera función es estrictamente creciente, mientras que la segunda es estrictamente decreciente; además ambas son simétricas respecto al eje 

Función exponencial natural
Esta se denota por  donde
donde  está dado por
está dado por

Esta notación fue introducida por Leonhard Euler hacia 1730, al descubrir muchas propiedades de este número. El número  es irracional y sus primeras diez cifras decimales son
es irracional y sus primeras diez cifras decimales son  .
.
Propiedades de la función exponencial
1 Dominio:  .
.
2 Recorrido:  .
.
3 Es continua.
4Los puntos  y
y  pertenecen a la gráfica.
pertenecen a la gráfica.
5 Es inyectiva  (ninguna imagen tiene más de un original).
(ninguna imagen tiene más de un original).
6 Creciente si  1}»>.
1}»>.
7 Decreciente si 0 < a < 1
8 Las curvas  y
y  son simétricas respecto al eje
son simétricas respecto al eje  .
.
9 La función exponencial  , con
, con  1}»> eventualmente crece más rápido que la función potencia
1}»> eventualmente crece más rápido que la función potencia  para cualquier
para cualquier  .
.
10 La función inversa de la función exponencial  es
es  . La función inversa de la exponencial natural es
. La función inversa de la exponencial natural es  .
.
Aplicaciones de la función exponencial
Las funciones exponenciales se emplean para modelar una amplia variedad de fenómenos como el crecimiento de poblaciones y las tasas de interés.
Crecimiento y decrecimiento exponencial
La fórmula que se emplea para modelar el crecimiento de una población viene dada por

La función  crece exponencialmente y representa la cantidad de la población a tiempo
crece exponencialmente y representa la cantidad de la población a tiempo  ;
;  representa la constante de crecimiento o decrecimiento; si
representa la constante de crecimiento o decrecimiento; si  se llama constante de crecimiento, mientras que si k < 0 se llama constante de decrecimiento.
se llama constante de crecimiento, mientras que si k < 0 se llama constante de decrecimiento.  representa la población inicial a tiempo cero, esto es,
representa la población inicial a tiempo cero, esto es,  .
.
La fórmula anterior se encuentra expresada en función de la exponencial natural, pero en algunas ocasiones se expresa con base  , esto es sencillo de obtener, basta aplicar las propiedades de los exponentes a
, esto es sencillo de obtener, basta aplicar las propiedades de los exponentes a  y considerar
y considerar  para obtener
para obtener

Ejemplo: Un grupo de investigadores estudian un cultivo de bacterias. Si al inicio de la observación se tienen  bacterias y media hora después se tienen
bacterias y media hora después se tienen  , encuentra:
, encuentra:
1 La cantidad de bacterias al cabo de dos horas.
2 La cantidad de bacterias al cabo de tres horas.
3 La tasa promedio de cambio de la población durante la segunda hora.
4 El tiempo requerido para duplicar la población inicial.
5 ¿Cuándo llegará la población a ser igual a  ?
?
Para poder responder a lo solicitado, primero necesitamos conocer en la fórmula de crecimiento poblacional  con
con  expresado en minutos.
expresado en minutos.
Notamos que conocemos la población inicial  , pero nos falta el valor de la constante de crecimiento. Para encontrar el valor de
, pero nos falta el valor de la constante de crecimiento. Para encontrar el valor de  utilizamos los datos del problema:
utilizamos los datos del problema:  en la fórmula de crecimiento
en la fórmula de crecimiento

Dividiendo ambos lados por  y aplicando la función inversa de la exponencial natural, se obtiene
y aplicando la función inversa de la exponencial natural, se obtiene

Así la función que modela el crecimiento de la población de bacterias es

1 La cantidad de bacterias al cabo de dos horas es

2 La cantidad de bacterias al cabo de tres horas

3 La tasa promedio de cambio de la población durante la segunda hora
Durante la segunda hora, el tiempo de  a
a  , la población cambió en
, la población cambió en  , por lo que la tas promedio en este periodo de tiempo es
, por lo que la tas promedio en este periodo de tiempo es

La población aumenta a la tasa promedio aproximada de  bacterias por minuto durante la segunda hora.
bacterias por minuto durante la segunda hora.
4 El tiempo requerido para duplicar la población inicial
Para esto empleamos la siguiente igualdad

Dividiendo ambos lados por  y aplicando la función inversa de la exponencial natural, se obtiene
y aplicando la función inversa de la exponencial natural, se obtiene

Así el tiempo requerido para que la población de bacterias se duplique es  minutos.
minutos.
5 ¿Cuándo llegará la población a ser igual a  ?
?
Para esto empleamos la siguiente igualdad

Dividiendo ambos lados por  y aplicando la función inversa de la exponencial natural, se obtiene
y aplicando la función inversa de la exponencial natural, se obtiene

Así el tiempo requerido para que la población de bacterias sea de  es de
es de  minutos.
minutos.
Interés compuesto
Se invierte una cantidad inicial de dinero  a una tasa de interés
a una tasa de interés  expresada en decimales. Si el interés se capitaliza una sola vez, entonces el saldo a obtener
expresada en decimales. Si el interés se capitaliza una sola vez, entonces el saldo a obtener  después de sumar el interés es
después de sumar el interés es

Si el interés se capitaliza más de una vez, el interés que se suma a la cuenta durante un periodo ganará interés durante los periodos siguientes. Si la tasa anual de interés es  y el interés se capitaliza
y el interés se capitaliza  veces por año, entonces al final de
veces por año, entonces al final de  años, el interés se capitalizó
años, el interés se capitalizó  veces y el saldo llamado valor futuro es
veces y el saldo llamado valor futuro es

Ejemplo: Si se invierten  a una tasa de
a una tasa de  anual. Hallar el valor futuro a
anual. Hallar el valor futuro a  años si el interés es compuesto trimestralmente.
años si el interés es compuesto trimestralmente.
Para encontrar el valor futuro después de  años si el interés se capitaliza trimestralmente, empleamos
años si el interés se capitaliza trimestralmente, empleamos  .
.
Sustituimos los valores en la fórmula del valor futuro

El saldo obtenido después de  años es de
años es de 
Interés compuesto continuamente
Para saber el saldo de una inversión al final de  años cuando la frecuencia de capitalización se incrementa sin límite, esto es, el interés no se capitaliza trimestral, ni mensual, ni diariamente, sino continuamente, se emplea la fórmula
años cuando la frecuencia de capitalización se incrementa sin límite, esto es, el interés no se capitaliza trimestral, ni mensual, ni diariamente, sino continuamente, se emplea la fórmula

Ejemplo: Si se invierten  a una tasa de
a una tasa de  anual. Hallar el valor futuro a
anual. Hallar el valor futuro a  años si el interés es compuesto continuamente.
años si el interés es compuesto continuamente.
Para encontrar el valor futuro después de  años si el interés se capitaliza continuamente, empleamos
años si el interés se capitaliza continuamente, empleamos  .
.
Sustituimos los valores en la fórmula del valor futuro

El saldo obtenido después de  años es de
años es de  y es el límite superior para el saldo posible.
y es el límite superior para el saldo posible.
Logaritmos y funciones logarítmicas
Definición de logaritmo
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener dicho número.


Siendo  la base,
la base,  el número e
el número e  el logaritmo.
el logaritmo.
Logaritmos decimales y neperianos
Los logaritmos decimales tienen base  . Se representan por
. Se representan por 
Los logaritmos neperianos (conocidos como logaritmos naturales) tienen  . Se representan por
. Se representan por  o
o 
Ejemplos de uso de la definición de logaritmo
Escribir los siguientes logaritmos en notación exponencial
1 
2 
3 
4 
Usando la definición de logaritmo y álgebra, calcular el valor de la incógnita en las siguientes ecuaciones
1 
Aplicamos la definición de logaritmo y pasamos el  a fracción decimal y la simplificamos:
a fracción decimal y la simplificamos:



El  lo ponemos en forma de potencia e igualamos los exponentes
lo ponemos en forma de potencia e igualamos los exponentes

2 
Aplicamos la definición de logaritmo y la raíz se pone en forma de potencia de exponente fraccionario


Igualamos los exponentes

3 
Aplicamos la definición de logaritmo y  se pasa a fracción decimal
se pasa a fracción decimal


El cociente lo pasamos a potencia de base  e igualamos los exponentes
e igualamos los exponentes

4 ![\displaystyle \log_{\sqrt{3}}\sqrt[5]{\frac{1}{81}}=y](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-0a6122e1c3ea93a87a6cf9299f7294db_l3.png)
Aplicamos la definición de logaritmo, las raíces se ponen en forma de potencia de exponente fraccionario y se igualan los exponentes
![Rendered by QuickLaTeX.com \displaystyle \left (\sqrt{3} \right )^{y}=\sqrt[5]{\frac{1}{81}}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-4bca0b5f241b5c23b14fa8b91cc4aba4_l3.png)


5 
Aplicamos la definición de logaritmo, teniendo en cuenta que la base del logaritmo neperiano es  .
.
La fracción se pone en forma de potencia y se igualan los exponentes



Propiedades de los logaritmos
1 El logaritmo de un producto es igual a la suma de los logaritmos de los factores


2 El logaritmo de un cociente es igual a la diferencia del logaritmo del dividendo y el logaritmo del divisor


3 El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base


4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz
![Rendered by QuickLaTeX.com \displaystyle \log\sqrt[n]{A} = \frac{\log A}{n} = \frac{1}{n}\cdot \log A](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-c85421036315669e7d770159a75e09ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \log_{2}(\sqrt[4]{8})=\frac{1}{4}\cdot \log_{2}(8)=\frac{1}{4}\cdot 3=\frac{3}{4}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-76bf9700f517ec604b0186ca9a417733_l3.png)
De las propiedades  y
y  podemos deducir que:
podemos deducir que:
![Rendered by QuickLaTeX.com \displaystyle \log\sqrt[n]{A^{m}} = \frac{m\cdot \log A}{n} = \frac{m}{n}\cdot \log A](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-9c4da73542f0bd0c73266e1d2d43edde_l3.png)
5 El logaritmo base » de » es .

6 El logaritmo de es (Sin importar la base del logaritmo)

Por lo tanto:


7 El argumento de un logaritmo siempre debe ser mayor que cero
Para  se cumple que
se cumple que  0″>
0″>
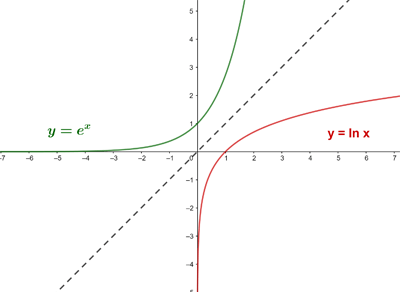
Función logarítmica
La función logarítmica en base  es la función inversa de la exponencial en base
es la función inversa de la exponencial en base  .
.


Ejemplos de funciones logarítmicas

 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |


 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |

Las propiedades de las funciones logarítmicas
- Dominio:

- Recorrido:

- Es continua
- Los puntos
 y
y  pertenecen a la gráfica.
pertenecen a la gráfica. - Es inyectiva (ninguna imagen tiene más de un original).
- Creciente si

- Decreciente si 0 < a < 1
Las gráfica de la función logarítmica es simétrica (respecto a la bisectriz del primer y tercer cuadrante) de la gráfica de la función exponencial, ya que son funciones reciprocas o inversas entre sí.

0 < a < 1

Funciones trigonométricas
Función seno
f(x) = sen x

Dominio: ℛ
Recorrido: [−1, 1]
Período: 2π rad
Continuidad: Continua en ∀x ∈ ℛ
Impar: sen(−x) = −sen x
Función coseno
f(x) = cos x

Dominio: ℛ
Recorrido: [−1, 1]
Período: 2π rad
Continuidad: Continua en ∀x ∈ ℛ
Par: cos(−x) = cos x
Función tangente
f(x) = tg x

Dominio: ℛ – {(2k + 1) · π/2, k ∈ℤ} = ℛ – {…,–π/2, π/2, 3π/2, …}
Recorrido: ℛ
Continuidad: Continua en: ∀ x ∈ ℛ – {π/2 + πk}
Período: π rad
Impar: tg(−x) = −tg x
Función cotangente
f(x) = cotg x

Dominio: ℛ – {k · π, k ∈ℤ} = ℛ – {…,–π, 0, π, …}
Recorrido: ℛ
Continuidad: Continua en: x ∈ ℛ – {πk, k ∈ ℤ}
Período: π rad
Impar: cotg(−x) = −cotg x
Función secante
f(x) = sec x
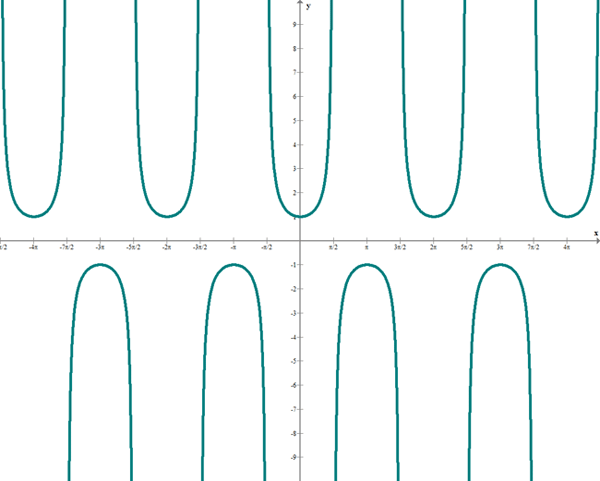
Dominio: ℛ – {(2k + 1) · π/2, k ∈ℤ} = ℛ – {…,–π/2, π/2, 3π/2, …}
Recorrido: (− ∞, −1] ∪ [1, ∞)
Período: 2π rad
Continuidad: Continua en ∀ x ∈ ℛ – {π/2 + πk}
Par: sec(−x) = sec x
Función cosecante
f(x) = cosec x

Dominio: ℛ – {(2k + 1) · π/2, k ∈ℤ} = ℛ – {…,–π/2, π/2, 3π/2, …}
Recorrido: (− ∞, −1] ∪ [1, ∞)
Período: 2π rad
Continuidad: Continua en: x ∈ ℛ – {πk, k ∈ ℤ}
Impar: cosec(−x) = −cosec x