Dos ecuaciones con dos incógnitas forman un sistema de ecuaciones y lo que pretendemos de ellas es encontrar su solución común

La solución de un sistema de ecuaciones es un par de números  tales que reemplazando
tales que reemplazando  por
por  ,
,  por
por  , se satisfacen a la vez ambas ecuaciones.
, se satisfacen a la vez ambas ecuaciones.
Ejemplo:
 es solución del sistema de ecuaciones
es solución del sistema de ecuaciones

1ºPara verificar que  es solución del sistema de ecuaciones, se deben satisfacer las igualdades de cada ecuación.
es solución del sistema de ecuaciones, se deben satisfacer las igualdades de cada ecuación.
2ºSustituimos  en el sistema de ecuaciones
en el sistema de ecuaciones



3ºComo se satisfacen ambas ecuaciones, concluimos que  es solución del sistema
es solución del sistema
Sistemas equivalentes
Criterios de equivalencia
1º Si a ambos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.


x = 2, y = 3
2º Si multiplicamos o dividimos ambos miembros de las ecuaciones de un sistema por un número distinto de cero, el sistema resultante es equivalente.


x = 2, y = 3
3º Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es equivalente al dado.


x = 2, y = 3
4º Si en un sistema se sustituye una ecuación por otra que resulte de sumar las dos ecuaciones del sistema previamente multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.


5º Si en un sistema se cambia el orden de las ecuaciones o el orden de las incógnitas, resulta otro sistema equivalente.


Método de sustitución
Los pasos del método de sustitución
Para resolver un sistema de ecuaciones por el método de sustitución seguiremos los siguientes pasos:
1º Se despeja una incógnita en una de las ecuaciones
2º Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita
3º Se resuelve la ecuación
4º El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada
5º Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de método de sustitución
Resuelve el siguiente sistema de ecuaciones

1º Despejamos una de las incógnitas en una de las dos ecuaciones.
Elegimos la incógnita que tenga el coeficiente más bajo

2º Sustituimos en la otra ecuación la variable x, por el valor anterior:

3 ºResolvemos la ecuación obtenida:






4º Sustituimos el valor obtenido en la variable despejada





5 ºSolución


El método de igualación
Pasos de resolución por el método de igualación
1º Despejamos la misma incógnita en ambas ecuaciones
2º Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3º Resolvemos la ecuación
4º Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5º Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1º Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2º Igualamos las expresiones:

3º Resolvemos la ecuación:






4º Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5º Solución:

Método de reducción
Pasos del método de reducción
Para resolver un sistema de ecuaciones por el método de reducción seguiremos los siguientes pasos:
1º Se preparan las dos ecuaciones, multiplicándolas por un numero tal que las ecuaciones resultantes tengan un coeficiente en común
2º Realizamos una resta (o suma según sea el caso de los signos de los coeficientes) para desaparecer (eliminar) una de las incógnitas
3º Se resuelve la ecuación resultante
4º El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve
5º Los dos valores obtenidos constituyen la solución del sistema
Ejemplos del método de reducción
En este caso, hay dos maneras de resolver el sistema de ecuaciones siguiente.
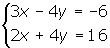
Por multiplicación
1º Eliminamos la x multiplicando la primera ecuación por 2 y la segunda por −3
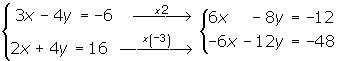
2º A la ecuación de arriba, le sumamos la ecuación de abajo y resolvemos la ecuación.
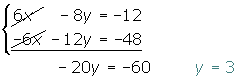
3º Sustituimos el valor de y en cualquiera de las 2 ecuaciones iniciales, en este caso la segunda.
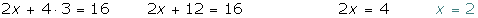
4º La solución es:
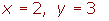
Sumando (o restando) las ecuaciones directamente
Como esta ecuación nos lo permite eliminar la  sin necesitar multiplicación, podemos hacer la suma de las ecuaciones sin prepararlas como en el método anterior.
sin necesitar multiplicación, podemos hacer la suma de las ecuaciones sin prepararlas como en el método anterior.
1º Sumamos miembro a miembro las ecuaciones:
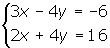



2º Sustituimos el valor de x en cualquiera de las 2 ecuaciones iniciales, en este caso la primera.






Podemos observar que en ambos casos, las soluciones son las mismas.