FUNCIONES

Definición de relación y de función

Para poder definir formalmente qué es una función, primero debemos definir una relación entre conjuntos.

Dados dos conjuntos y , llamamos relación de $\quad A \quad$ en $\quad B \quad$ cualquier correspondencia que haya entre algunos de los elementos de $\quad A \quad$ con los elementos de $\quad B$ .

Ejemplos

1. Consideremos los conjunto $\quad A = \{ -1, 3, 6, 2 \} \quad$ y $\quad B = \{ 1, -1, 3, -3, 6, -6, 5, 9\} \quad$ , y la relación dada por la siguiente imagen

representacion grafica de relacion entre los conjuntos A y B

Notemos que no todos los elementos de $\quad A \quad$ están relacionados con elementos de $\quad B$ , por ejemplo, el elemento $\quad 2 \in A \quad$ no tiene imagen en $\quad B$ .

Nota. En una relación no es necesario que todos los elementos de ambos conjuntos estén relacionados.

También podemos escribir la relación como un conjunto, en este caso la relación estaría dada por el conjunto $\quad R = \{ (-1, 1), (-1, -1), (3, -3), (3, 3), (6, -6), (6, 6)\}$ . Notemos que, para cada par ordenado, la primer entrada, contando de izquierda a derecha, es un elemento de $\quad A$ , mientras que el de la segunda entrada es el elemento de $\quad B \quad$ con el cual se relaciona.

2.Consideremos los conjunto $\quad A = \{ -2, -1, 0, 1, 2 \} \quad$ y $\quad B = \{0, 1, 4\} \quad$ , y la relación dada por la siguiente imagen

la relacion entre los conjuntos A y B representacion grafica

En este caso, todos los elementos de $\quad A \quad$ están relacionados con elementos de $\quad B$ .

Esta relación dada como conjunto estaría dada por $\quad R = \{ (0, 0), (1, 1), (-1, 1), (2, 4), (-2, 4)\}$ .

Ahora que sabemos qué es una relación, podemos definir una función entre conjuntos.

Dados dos conjuntos $\quad A \quad$ y $\quad B$ , una función de $\quad A \quad$ en $\quad B \quad$ es una relación que cumple las siguientes dos propiedades:

Todo elemento del conjunto $\quad A \quad$ debe de estar relación con un elemento del conjunto $\quad B$ .

Ningún elemento del conjunto $\quad A \quad$ debe de estar relación con mas de un elemento del conjunto $\quad B$ .

Estas dos propiedades pueden reducirse a decir que todo elemento del conjunto $\quad A \quad$ debe de estar relación con un único elemento del conjunto $\quad B$ .

Dada una función de un conjunto $\quad A \quad$ en un conjunto $\quad B$ , al conjunto $\quad A \quad$ se le conoce como dominio, mientras que al conjunto $\quad B \quad$ como codominio (o contradominio).

Usualmente a una función se le denota por $\quad f \quad$ y para denotar que esta va de un conjunto $\quad A \quad$ en un conjunto $\quad B \quad$ escribimos

$f: A \to B$ .

Además, si $\quad x \quad$ es un elemento en $\quad A \quad$ , entonces, al elemento con el cual se relaciona en $\quad B \quad$ lo denotamos por

y = f(x) ,

esto lo podemos interpretar como $\quad x \quad$ el cual se relaciona con $\quad y \quad$ bajos las reglas dadas por $\quad f \quad$ .

Cuando utilizamos la notación $\quad y = f(x)$ , a $\quad x \quad$ la conocemos como la variable independiente, mientras que a $\quad y \quad$ la conocemos como la variable dependiente.

Ejemplos

1. El ejemplo 1 de relaciones no es una función ya que hay elementos del dominio, $\quad A$ , que no están relacionados con ningún elemento del codominio, $\quad B$ . Además, hay elementos en $\quad A$ que se relacionan con más de un elemento en $\quad B$ .

2. El ejemplo 2 de relaciones sí es una función ya que todos los elementos del dominio, $\quad A$ , están relacionados con un único elemento del codominio, $\quad B$ . De hecho, en este caso, podemos ver que, para todo $\quad x \in A$ , su relación con los elementos $\quad y \in B \quad$ está dada por $\quad y = f(x) = x^2$ .

3. Consideremos el conjunto $\quad A = \mathbb{N} \quad$ , al conjunto $\quad B = \mathbb{R} \quad$ y a $\quad f: \mathbb{N} \to \mathbb{R} \quad$ dada por $\quad y = f(x) = \sqrt{x} \quad$ . ¿Es una función? Bueno, eso depende, veamos por qué.

representacion grafica de relacion entre conjuntos A y B

Primero, notemos que para todo número, por ejemplo, $\quad 9 \quad$ , se tiene que $\quad \sqrt{9} = \pm 3$ , esto ya que $\quad 3^2 = (-3)^2 = 9$ . Por lo tanto, en este caso, para cada elemento del dominio le estaríamos asignando dos elementos del codiminio y no sería una función.

Sin embargo, cuando se habla de la raíz de un número, solemos considerar únicamente la parte positiva, por lo tanto, a menos que se especifique lo contrario, para todo número, por ejemplo, $\quad 9 \quad$ , se tendrá que $\quad \sqrt{9} = 3$ . Así, tendríamos que $\quad f(x) = \sqrt{x} \quad$ sí es una función ya que por lo mencionado tendríamos una única correspondencia para todo elemento en el dominio, además, como definimos de un inicio $\quad f: \mathbb{N} \to \mathbb{R}$ ya estamos considerando todo el dominio $\quad \mathbb{N}$ .

Si queremos considerar únicamente la parte negativa de la raíz, debemos definir $\quad f(x) = -\sqrt{x} \quad$ , en este caso, al igual que en el anterior, también tendríamos una función.

Si una función cumple que tanto su dominio como su codominio son subconjuntos de los reales ( $A, B \subseteq \mathbb{R}$ ), entonces decimos que tenemos una función real.

Explicación del dominio de una función

El dominio de una función está formado por todos los elementos que tienen imagen.

Es decir, son los valores de que podemos sustituir en la regla de correspondencia de una función para obtener el valor correspondiente de f(x) .Matemáticamente, podemos expresar:

D=\left \{ x\, \epsilon \, \mathbb{R}\, /\, \exists \, f(x) \right \}

que significa que el dominio de una función son aquellos valores de que pertenecen a los números reales para los cuales existe un valor asociado de la función f(x) .

El subconjunto de los números reales en el que se define la función se llama dominio o campo existencia de la función.

Se designa por D.

La variable x perteneciente al dominio de la función recibe el nombre de variable independiente.

Conjunto inicial Conjunto final

Dominio Conjunto imagen o recorrido

Dominio de la función polinómica entera

El dominio de una función polinómica es $\mathbb{R}$ , porque cualquier número real tiene imagen.

También son funciones polinómicas enteras las que tienen un número (una constante) en el denominador:

Ejemplos de dominios de las funciones polinómicas

1 $f(x)=x^{2}-5x+6$ $D=\mathbb{R}$

2 $f(x)=\frac{x^{2}-25}{5}$ $D=\mathbb{R}$

Puedes probar que al sustituir cualquier valor de en las funciones siempre obtendrás un valor correspondiente para f(x) .

Dominio de la función racional

El dominio es $\mathbb{R}$ menos los valores que anulan al denominador (no puede existir una fracción cuyo denominador sea cero)..

Ejemplo de ejercicio de dominio de la función racional

1 ¿Qual es el dominio de la función $f(x)=\frac{2x-5}{x^{2}-5x+6}$ ?

Igualamos el denominador a y resolvemos la ecuación

x=\cfrac{5\pm \sqrt{5^{2}-4\cdot 6}}{2}=\cfrac{5\pm \sqrt{25-24}}{2}=\cfrac{5\pm 1}{2}=\cfrac{5\pm 1}{2}

Dominio de la función radical de índice impar

El dominio es el dominio de la función radicando.

1 $f(x)=\sqrt[3]{x^{2}-5x+6}$ $D=\mathbb{R}$

2 $f(x)=\sqrt[3]{\cfrac{x}{x^{2}-5x+6}}$ $D=\mathbb{R}-\left \{ 2,3 \right \}$

Dominio de la función radical de índice par

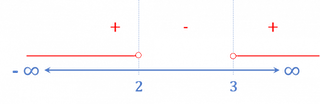
El dominio está formado por todos los valores del radicando que hacen que éste sea mayor o igual que cero.

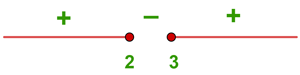
Ejemplo de intervalos cerrados por un extremo representacion grafica

\left\{\begin{matrix} x^{2}-5x+6\geq 0 \; \; \; \; \; \; \; \;& \Rightarrow & \; \; \; \; \; \; (-\infty ,2]\cup [3,\infty ) \\ &\\ \; \; x+4\neq 0 & \Rightarrow & x\neq -4 \end{matrix}\right.

D=(-\infty ,-4)\cup (-4,2]\cup [3,\infty )

3¿Cuál es el dominio de la función $f(x)=\sqrt{x^{2}-5x+6}$ ?

En este caso, el denominador debe ser mayor que cero y, además, debemos buscar los valores de para que la raíz exista, por lo que:

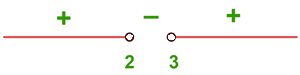
Ejemplo de un intervalo abierto representacion grafica

4Determinar el dominio de la función $f(x)=\sqrt{\cfrac{x+4}{x^{2}-5x+6}}$ .

El radicando tiene que ser mayor que cero y el denominador distinto de cero

\left\{\begin{matrix} \cfrac{x+4}{x^{2}-5x+6}\geq 0 \\ & & \\ x^{2}-5x+6\neq 0 \end{matrix}\right.

Signos de la función en distintos intervalos representacion grafica

5 Obtener el dominio de la función $f(x)=\sqrt{x^{2}-5x-14}$ .

Como el radicando debe ser mayor o igual que cero, planteamos la desigualdad:

Resolvemos la inecuación de segundo grado

Las raíces de la ecuación de segundo grado asociada a la desigualdad son: x=-2 y x=7

Por lo que los intervalos en los que se cumple la desigualdad serían: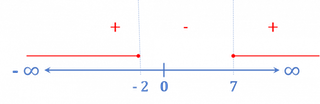 Visualizar el intervalo solución de la desigualdad propuesta

El dominio lo forman los valores menores que el -2 y mayores que 7, incluyéndolos.

6 Obtener el dominio de la función $f(x)=\frac{\sqrt{x^{2}-10x+24}}{x+5}$ .

En este caso se deben cumplir dos condiciones, una para el cociente y otra para la raíz, por lo que el numerador tiene que ser mayor o igual que cero y el denominador distinto de cero. Por lo que:

\left\{\begin{matrix} x^{2}-10x+24\geq 0\\ x+5\neq 0 \end{matrix}\right.

\begin{matrix} (-\infty ,4]\cup [6,\infty )\\ x\neq -5 \end{matrix}

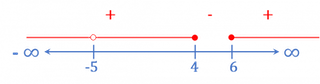
Representación gráfica del dominio de la función

D=(-\infty ,-5)\cup (-5,4]\cup [6,\infty )

Dominio de la función logarítmica

El dominio está formado por todos los valores que hacen que la función que aparece dentro del logaritmo sea mayor que cero.

Se debe cumplir:

Representación gráfica del dominio de la función

Dominio de la función exponencial

Ejemplos de dominio de funciones exponenciales

1 $f(x)=e^{x^{2}-1}$ $D=\mathbb{R}$

2 $f(x)=e^{\frac{1}{x}}$

El dominio es igual a $\mathbb{R}$ menos los valores que anulan el denominador del exponente

3 $f(x)=e^{\sqrt{x^{2}-5x+6}}$

El dominio coincide con el campo de existencia real de la raíz

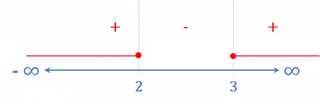
Representación del dominio de la función

Función inversa

Definición de la función inversa

Se llama función inversa o reciproca de $\displaystyle f(x)$ a otra función $\displaystyle f^{-1}(x)$ que cumple que:

Si $\displaystyle f(a)=b$ , entonces $\displaystyle f^{-1}(b)=a$

Veamos un ejemplo a partir de la función $\displaystyle f(x)=x+4$

Podemos observar que:

El dominio de $\displaystyle f^{-1}(x)$ es el recorrido de $\displaystyle f(x)$ .
El recorrido de $\displaystyle f^{-1}(x)$ es el dominio de $\displaystyle f(x)$ .

Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.

Si dos funciones son inversas su composición es la función identidad.

\displaystyle (fo f^{-1})(x)=(f^{-1}of)(x)=x

Las gráficas de $\displaystyle f(x)$ y $\displaystyle f^{-1}(x)$ son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, $\displaystyle f^{-1}(x)$ , y la inversa de una función: $\displaystyle \frac{1}{f(x)}$ .

La inversa de la función $\displaystyle f(x)=x+4$ es

$\displaystyle \frac{1}{x+4}$ .

La función inversa de $\displaystyle f(x)=x+4$ es $\displaystyle f^{-1}(x)=x-4$ porque la composición de las dos funciones es la función identidad

\displaystyle g\cdot f=g\left [ f(5) \right ]=g\left ( x+4 \right )=x+4-4=x

Cálculo de la función inversa

Para construir o calcular la función inversa de una función cualquiera, se deben seguir los siguientes pasos:

Paso 1: Se escribe la función con $\displaystyle x$ e $\displaystyle y$ .

Paso 2: Se despeja la variable $\displaystyle x$ en función de la variable $\displaystyle y$ .

Paso 3: Se intercambian las variables.

Ejemplos con ejercicios resueltos

Calcular la función inversa de:

1 $\displaystyle f(x)=\frac{2x+3}{x-1}$

Cambiamos $\displaystyle f(x)$ por $\displaystyle y$

Quitamos denominadores

Resolvemos el paréntesis

pasamos al primer miembro las $\displaystyle x$

Extraemos el factor común, es decir, la $\displaystyle x$

Ahora despejamos la $\displaystyle x$

Cambiamos x por $\displaystyle f^{-1}(x)$ y obtendremos la función inversa

Vamos a comprobar el resultado para $\displaystyle x=2$

Como $\displaystyle f(2)$ nos resulta $\displaystyle 7$ y $\displaystyle f^{-1}(7)$ nos resulta $\displaystyle 2$ , eso significa que la función inversa es correcta

2 $\displaystyle f(x)=\sqrt[3]{x-1}$

Cambiamos $\displaystyle f(x)$ por $\displaystyle y$

Elevamos al cubo en los dos miembros

Despejamos la $\displaystyle x$ y cambiamos $\displaystyle x$ por $\displaystyle f^{-1}(x)$

3 $\displaystyle f(x)=x^{2}$

Cambiamos $\displaystyle f(x)$ por $\displaystyle y$

Despejamos la $\displaystyle x$

No es una función.

No existe función inversa porque cualquier elemento tiene dos imágenes y una función puede tener a lo sumo una imagen

Funciones acotadas

Función acotada superiormente

Una función f está acotada superiormente si existe un número real k tal que para toda x es f(x) ≤ k.

El número k se llama cota superior.

Ejemplo

k=0.135

Función acotada inferiormente

Una función f está acotada inferiormente si existe un número real k′ tal que para toda x es f(x) ≥ k′.

El número k′ se llama cota inferior.

k′ = 2

Función acotada

Una función esta acotada si lo está a superior e inferiormente.

k’ ≤ f(x) ≤ k

k = ½ k′ = -½

Máximos y mínimos relativos y absolutos

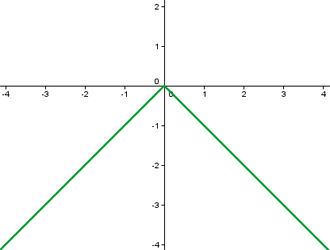
representación gráfica de función con máximo absoluto en 0

Mínimo absoluto

Una función tiene su mínimo absoluto en {x=b} si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.

En la siguiente gráfica, la función tiene su mínimo absoluto en {x=4}

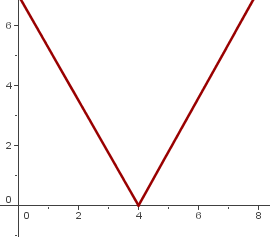
representación gráfica de función con mínimo absoluto en 4

Máximo y mínimo relativo

Una función {f(x)} tiene un máximo relativo en {x=a} , si {f(a)} es mayor o igual que los puntos próximos a {a} .

Una función {f(x)} tiene un mínimo relativo en {x=b} , si {f(b)} es menor o igual que los puntos próximos a {b} .

Cálculo de máximos y mínimos relativos

El siguiente método es conocido como el criterio de la segunda derivada

1Calculamos la primera y segunda derivada de la función {f(x)} .

2Igualamos la primera derivada a cero y despejamos la variable {x} . Este resultado es conocido como puntos críticos.

3Sustituimos los puntos críticos en la segunda derivada:

Si el resultado es positivo, entonces decimos que la función posee un mínimo en el punto crítico.

Si el resultado es negativo, entonces decimos que la función posee un máximo en el punto crítico.

Si el resultado es cero, entonces no podemos concluir y se tiene que emplear el criterio de la primera derivada.

4Sustituimos los puntos críticos donde la función alcanza su máximo o mínimo relativo en la función original. El resultado obtenido es conocido como valor crítico.

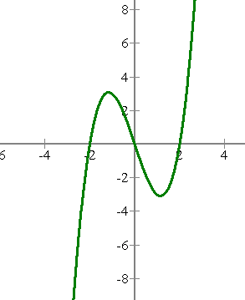
Ejemplo de cálculo de máximo y mínimo de una función

Encuentra los extremos relativos de ${f(x)=x^{3}-4x}$

1Calculamos la primera y segunda derivada de la función {f(x)} .

2Buscamos los puntos críticos

{\begin{array}{rcl} 3x^{2}-4&=&0 \\ && \\ x^{2}&=& \displaystyle\frac{4}{3}\\ && \\ x&=&\pm \sqrt{\displaystyle\frac{4}{3}} \\ && \\ x&=& \pm \displaystyle\frac{2\sqrt{3}}{3} \end{array}}

3Sustituimos los puntos críticos en la segunda derivada:

{f''\left( \displaystyle\frac{2\sqrt{3}}{3}\right)=4\sqrt{3}>0}

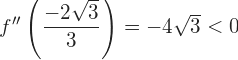
Concluimos que la función posee un mínimo en ${x=\displaystyle\frac{2\sqrt{3}}{3}}$ .

Concluimos que la función posee un máximo en ${x=-\displaystyle\frac{2\sqrt{3}}{3}}$ .

4Calculamos los valores críticos

{f\left( \displaystyle\frac{2\sqrt{3}}{3}\right)=\displaystyle\frac{8\sqrt{3}}{9}-\frac{8\sqrt{3}}{3}=-\frac{16\sqrt{3}}{9}}

representación gráfica de función -2 y 2

Funciones simétricas

Respecto del eje de ordenadas. Función par

Una función f es simétrica respecto del eje de ordenadas cuando para todo x del dominio se verifica:

f(−x) = f(x)

Las funciones simétricas respecto del eje de ordenadas reciben el nombre de funciones pares.

Ejemplo

Comprobar que la siguiente función es par:

Simetría respecto al origen. Función impar

Una función f es simétrica respecto al origen cuando para todo x del dominio se verifica:

f(−x) = −f(x)

Las funciones simétricas respecto al origen reciben el nombre de funciones impares.

Ejemplo

Comprobar que la siguiente función es impar:

Funciones periódicas

Una función f(x) es periódica, de período T, si para todo número entero z, se verifica:

f(x) = f(x + zT)

Estudio de funciones periodicas

Función seno

La función f(x) = sen x es periódica de periodo 2π, ya que cumple que:

sen (x + 2π) = sen x

Función tangente

La función f(x) = tg x es periódica de periodo π, ya que cumple que:

tg (x + π) = tg x

Función mantisa

La función mantisa, f(x) = x – E(x), es periódica de periodo 1.

Cálculo del periodo

Si tenemos una función periódica f(x) de periodo T, la función g(x) = f(kx) tiene de periodo:

Ejemplos

Hallar el periodo de las funciones:

1. f(x) = sen 2x

2. f(x) = tg (1/2)x

3. f(x) = E (1/2)x

Teoría de las Funciones II

tipos de funciones y su clasificación imagen

Las funciones algebraicas

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

Las funciones algebraicas pueden ser:

Funciones explícitas

Si se pueden obtener las imágenes de por simple sustitución como en este ejemplo : f(x)=5x-2

Funciones implícitas

Si no se pueden obtener las imágenes de por simple sustitución, sino que es necesario efectuar operaciones, como en este ejemplo 5x - y - 2 = 0

Ademas de esta clasificación, hay 6 otros tipos de funciones algebraicas

1 Funciones polinómicas

Son las funciones que vienen definidas por un polinomio.
$f(x)=a_0+a_1x+a_2x+a_3x+...+a_nx^{n}$
Su dominio es $\mathbb{R}$ , es decir, cualquier número real tiene imagen.

2 Funciones constantes

El criterio viene dado por un número real.
La gráfica es una recta horizontal paralela a al eje de abscisas.

3 Funciones polinomicas de primer grado

1 f(x) = mx + n

Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
Son funciones de este tipo las siguientes:
Función afín

2 f(x) = mx

Función lineal

3 f(x) = x

Función identidad

4 f(x) = ax² + bx + c

Funciones cuadráticas
Son funciones polinómicas de segundo grado,
La gráfica de una función polinómica es una parábola.

4 Funciones racionales

\displaystyle f(x)=\frac{a_0+a_1x+a_2x^{2}+...+a_nx^{n}}{b_0+b_1x+b_2x^{2}+...+b_mx^{m}}

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
El criterio viene dado por un cociente entre polinomios:

5 Funciones radicales

El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es $\mathbb{R}$ .
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.

6 Funciones algebraicas a trozos

Son funciones definidas por distintos criterios, según los intervalos que se consideren.

Funciones en valor absoluto

Función parte entera de x

Función mantisa

Función signo

Las funciones trascendentes

La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

1 Funciones exponenciales

Sea a un número real positivo. La función que a cada número real le hace corresponder la potencia $a^{x}$ se llama función exponencial de base y exponente .