TEORÍA VECTORES

Definición de vector:

Un vector fijo  es un segmento orientado que va del punto A (origen) al punto B (extremo).

Módulo del vector:

Es la longitud del segmento AB, se representa por 

Dirección y sentido del vector:

Dirección de un vector:

Es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

Sentido del vector: 

El que va del origen A al extremo B.

Vectores opuestos:

Dos puntos A y B determinan dos vectores fijos  y , con sentido distinto, que se llaman vectores opuestos.

Vector nulo:

Un vector fijo es nulo cuando el origen y su extremo coinciden.

Vectores equipolentes

Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.

Si  y  son vectores equipolentes, el cuadrilátero ABCD es un paralelogramo.

Ejemplo:

Calcula las coordenadas de C para que el cuadrilátero de vértices: A(-3, -4), B(2, -3), D(3, 0) y C; sea un paralelogramo.

Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.

Si  y  son vectores equipolentes, el cuadrilátero ABCD es un paralelogramo.

Ejemplo:

Calcula las coordenadas de C para que el cuadrilátero de vértices: A(-3, -4), B(2, -3), D(3, 0) y C; sea un paralelogramo.

ectores libres

El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Cada vector fijo es un representante del vector libre.

1 Vector de posición de un punto en el plano de coordenadas

El vector  que une el origen de coordenadas O con un punto P se llama vector de posición del punto P.

2 Coordenadas o componentes de un vector en el plano

Si las coordenadas de A y B son:

Las coordenadas o componentes del vector  son las coordenadas del extremo menos las coordenadas del origen.

Ejemplo:

Hallar las componentes de un vector cuyos extremos son:

Un vector  tiene de componentes (5, −2). Hallar las coordenadas de A si se conoce el extremo B(12, −3).

Módulo de un vector

El módulo de un vector es la longitud del segmento orientado que lo define.

El módulo de un vector es un número siempre positivo y solamente el vector nulo tiene módulo cero.

Tenemos dos modos de calcularlo:

1 Cálculo del módulo conociendo sus componentes.

2 Cálculo del módulo conociendo las coordenadas de los puntos.

Cálculo del módulo conociendo sus componentes

Si conocemos los componentes del vector, la fórmula a usar es la siguiente:

\vec u = \left ( u_1, u_2 \right )
\left | \vec u \right | = \sqrt{u_1^{2},+u_2^{2}}

Ejemplo

1  \vec u = \left ( 3,4 \right ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left | \vec u \right |= \sqrt {3^{2},4^{2}}= \sqrt 25=5

Cálculo del módulo conociendo las coordenadas de los puntos

Si conocemos el punto inicial y punto final del vector, la fórmula a usar es la siguiente:

A(x_1,y_1)\ \ \ \ \ \ \ \ \ \ B(x_2, y_2)
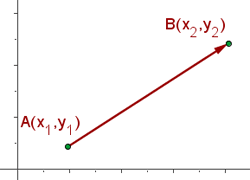
gráfica de un vector A(x1, y2) y B(x2,y2)
\left | \vec AB \right |=\sqrt \left ( x_2-x_1 \right )^{2}+\left ( y_2-y_1 \right ))^{2}

Ejemplo

1  A(2,1)\ \ \ \ \ \ \ \ \ \ B(-3, 2)\ \ \ \ \ \ \ \ \ \ \left | \vec AB \right |=\sqrt \left ( -3-2 \right )^{2}+\left ( 2-1 \right )^{2}=   \sqrt 26

Distancia entre dos puntos

La distancia entre dos puntos es igual al módulo del vector que tiene de extremos dichos puntos.

A(x_1,y_1)\ \ \ \ \ \ \ \ \ \ B(x_2, y_2)
d(A,B)=\sqrt \left ( x_2-x_1 \right )^{2}+\left ( y_2-y_1 \right )^{2}

Ejemplo

1 A(2,1)\ \ \ \ \ \ \ \ \ \ B(-3, 2)\ \ \ \ \ \ \ \ \ \d(A,B)=\sqrt \left ( -3-2 \right )^{2}+\left (2-1 \right )^{2}=  \sqrt 26

Sea \vec{v} un vector diferente de cero, dicho vector tiene  alguna magnitud, dirección y sentido. En muchas ocasiones por razones de simplificación de cálculos, es necesario generar a otro vector que tenga la misma dirección y sentido que \displaystyle \vec{v}, pero con magnitud uno (unitario), por esta razón hacemos uso de un proceso llamado normalización.

Normalizar un vector

Normalizar,  consite en tomar a un vector \displaystyle \vec{v} distinto de cero, y con él obtener un vector \displaystyle \vec{u}, de la misma dirección y sentido que \displaystyle \vec{v} pero con magnitud uno.

  • Primero tomamos a un vector \displaystyle\vec{v}=(v_1,v_2) diferente de cero
  • Ahora calculamos su magnitud ( la cual debe ser diferente de cero)
\displaystyle \left \| \vec{v} \right \|=\sqrt{v_1^2+v_2^2}
  • Mutiplicamos a \displaystyle\vec{v} por el recíproco de la magnitud, y el vector que nos queda es \vec{u}
\displaystyle \vec{u}=\frac{1}{\left \| \vec{v} \right \|}\vec{v}

Comprobemos entonces que la magnitud de \displaystyle \vec{u} es uno.

\displaystyle \left \| \vec{u} \right \|=\left \| \frac{1}{\left \| \vec{v} \right \|} \vec{v} \right \|=\left \| \frac{1}{\left \| \vec{v} \right \|} \left ( v_1,v_2 \right ) \right \|=\left \| \left ( \frac{v_1}{\left \| \vec{v} \right \|},\frac{v_2}{\left \| \vec{v} \right \|} \right ) \right \|
\displaystyle\left \| \vec{u} \right \|=\left \| \left ( \frac{v_1}{\left \| \vec{v} \right \|},\frac{v_2}{\left \| \vec{v} \right \|} \right ) \right \|=\sqrt{\left ( \frac{v_1}{\left \| \vec{v} \right \|} \right )^2+\left ( \frac{v_2}{\left \| \vec{v} \right \|} \right )^2}
\displaystyle \left \| \vec{u} \right \|=\sqrt{\left ( \frac{v_1}{\left \| \vec{v} \right \|} \right )^2+\left ( \frac{v_2}{\left \| \vec{v} \right \|} \right )^2}=\sqrt{\frac{v_1^2}{\left \| \vec{v} \right \|^2}+\frac{v_2^2}{\left \| \vec{v} \right \|^2}}=\sqrt{\frac{v_1^2+v_2^2}{\left \| \vec{v} \right \|^2}}
\displaystyle \left \| \vec{u} \right \|=\sqrt{\frac{v_1^2+v_2^2}{\left \| \vec{v} \right \|^2}}=\frac{\sqrt{v_1^2+v_2^2}}{\left \| \vec{v} \right \|}=\frac{\left \| \vec{v} \right \|}{\left \| \vec{v} \right \|}=1

esto comprueba que el vector obtenido tiene las características deseadas

Ejemplos de problemas de normalización

1Si \vec{v}=(3,4), hallar un vector unitario de su misma dirección y sentido.

Solución:

\displaystyle \left \| \vec{v} \right \|=\sqrt{3^{2}+4^2}=\sqrt{9+16}=\sqrt{25}=5

entonces

\displaystyle \vec{u}=\frac{1}{5}\left ( 3,4 \right )= \left ( \frac{3}{5},\frac{4}{5} \right )

Es importante mencionar que el proceso también es válido para dimensiones \displaystyle n\geq 2, como se analiza en el siguiente ejemplo.

2Si \displaystyle\vec{v}=(3,-2,9), hallar un vector unitario de su misma dirección y sentido.

Solución:

\displaystyle \left \| \vec{v} \right \|=\sqrt{3^2+(-2)^2+9^2}=\sqrt{9+4+81}= \sqrt{94}

entonces

\displaystyle \vec{u}=\frac{1}{\sqrt{94}}\left ( 3,-2,9 \right )= \left ( \frac{3}{\sqrt{94}},\frac{-2}{\sqrt{94}},\frac{9}{\sqrt{94}} \right )

Suma de vectores

La operación de suma de dos o más vectores da como resultado otro vector. Para realizar la suma de vectores existen distintos métodos, ya sea de manera algebraica o mediante el uso de geometría analítica.

El método algebraico es conocido como método directo.

Los métodos usando geometría analítica son conocidos como, el método del polígono que es utilizado para sumar más de dos vectores, el método del triángulo es el caso particular del método del polígono cuando únicamente se suman dos vectores, y el método del paralelogramo igualmente para sumar dos vectores.

Método algebraico

1Método directo

Para sumar dos o más vectores se suman sus respectivas componentes de cada vector.

En el caso de dos vectores, la suma se realiza de la siguiente forma:

\vec u = (u_{1}, u_{2})
\vec v = (v_{1}, v_{2})
\vec u + \vec v= (u_{1}+v_{1}, u_{2}+u_{2})

Ejemplo

\vec u = (-2, 5)
\vec v = (3, -1)
\vec u+\vec v = (-2+3, 5-1)=(1,4)

Métodos con geometría analítica

1Método del triángulo

Representación gráfica de la resta de vectores por el método del triángulo

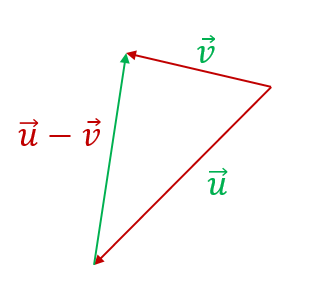
Para sumar dos vectores libres \vec u  y \vec v  se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.

2Método del paralelogramo

Representación gráfica del método del paralelogramo

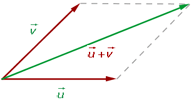
Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.

3Método del polígono

Representación gráfica del método del polígono suma

El método del polígono es utilizado cuando queremos sumar más de dos vectores, y consiste en colocar un vector a continuación del otro, de modo que el extremo de uno coincida con el origen del otro, y así sucesivamente, hasta colocar todos los vectores, la resultante será el vector que cierra el polígono, es decir, es aquel que va desde el inicio del primero al extremo del último vector.

Resta de vectores

La operación de resta de dos o más vectores da como resultado otro vector. Para realizar la resta de vectores existen distintos métodos, ya sea de manera algebraica o mediante el uso de geometría analítica.

El método algebraico es conocido como método directo.

Los métodos usando geometría analítica son conocidos como, el método del polígono que es utilizado para restar más de dos vectores, el método del triángulo es el caso particular del método del polígono cuando únicamente se restan dos vectores, y el método del paralelogramo igualmente para restar dos vectores.

Método algebraico

1Método directo

Para restar dos vectores libres \vec u  y \vec v  se suma \vec u  con el opuesto de \vec v .

Las componentes del vector resta se obtienen restando las componentes de los vectores.

\vec u = (u_{1}, u_{2})
\vec v = (v_{1}, v_{2})
\vec u - \vec v = (u_{1}-v_{1}, u_{2}-v_{2})

Ejemplo

\vec u = (-2, 5)
\vec v = (3, -1)
\vec u - \vec v = (-2-3, 5-(-1))=(-5,6)

Métodos con geometría analítica

1Método del triángulo

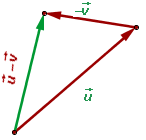
Representación gráfica del método del triángulo resta

Para restar dos vectores libres \vec u  y \vec v  se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.

2Método del paralelogramo

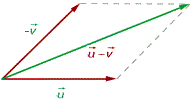
Representación gráfica del método del paralelogramo resta

Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.

3Método del polígono

El método del polígono es utilizado cuando queremos restar más de dos vectores, y consiste en colocar un vector a continuación del otro, de modo que el extremo de uno coincida con el origen del otro, y así sucesivamente, hasta colocar todos los vectores, la resultante será el vector que cierra el polígono, es decir, es aquel que va desde el inicio del primero al extremo del último vector.

Propiedades de la suma y resta de vectores

1 Asociativa

\vec u + (\vec v + \vec w)= (\vec u + \vec v)+ \vec w

2 Conmutativa

\vec u + \vec v = \vec v + \vec u

3 Elemento neutro

\vec u + \vec 0 = \vec u

4 Elemento opuesto

\vec u +(- \vec u )= \vec 0

El producto de un número k por un vector es otro vector:

1 De igual dirección que el vector .

2 Del mismo sentido que el vector  si k es positivo.

3 De sentido contrario del vector  si k es negativo.

4 De módulo 

Las componentes del vector resultante se obtienen multiplicando por K las componentes del vector.

Ejemplo:

Propiedades del producto de un número por un vector

1 Asociativa

k · (k’ ·  ) = (k · k’) · 

2 Distributiva respecto a la suma de vectores

k · (  +  ) = k ·  + k · 

3 Distributiva respecto a los escalares

(k + k’) ·  = k ·  + k’ · 

4 Elemento neutro

1 ·  = 

¿Cómo encontramos el punto medio de un segmento?

Ejercicio de coordenadas del punto medio de un segmento

Si las coordenadas de los puntos extremos de un segmento {AB} son {A=(x_1,y_1)} y {B=(x_2,y_2)}, las coordenadas del punto medio del segmento coinciden con la semisuma de las coordenadas de de los puntos extremos.

Fórmulas para las coordenadas del punto medio de un segmento

{x_{m}=\displaystyle\frac{x_{1}+x_{2}}{2} \ \ \ \ \ \ y_{m}=\displaystyle\frac{y_{1}+y_{2}}{2}}

Ejemplo de ejercicios con el punto medio de un segmento

Hallar las coordenadas del punto medio del segmento {AB} con extremos {A=(3,9)} y {B=(-1,5)}.

1Sustituimos los valores extremos en la fórmula delas coordenadas del punto medio

{x_{m}=\displaystyle\frac{3-1}{2}=1 \ \ \ \ \ \ y_{m}=\displaystyle\frac{9+5}{2}=7}

2El punto medio es {(1,7)}.

Condición para qué tres puntos estén alineados

Ejemplo de tres puntos alineados

Tres puntos {A (x_{1}, y_{1}), B(x_{2}, y_{2})} y {C(x_{3}, y_{3})} están alineados siempre que los vectores {\overrightarrow{AB}} y {\overrightarrow{BC}} tengan la misma dirección. Esto ocurre cuando sus coordenadas son proporcionales.

{\displaystyle\frac{x_{2}-x_{1}}{x_{3}-x_{2}}=\frac{y_{2}-y_{1}}{y_{3}-y_{2}}}

Ejemplos de ejercicios con puntos alineados 

1Calcular el valor de {a} para que los puntos estén alineados

{A (2, 1), \; B(4, 2),\; C(6, a)}

Para que estén alineados se requiere que sus coordenadas sean proporcionales

{\displaystyle\frac{4-2}{6-4}=\frac{2-1}{a-2} \ \ \ \Longrightarrow \ \ \ a=3}

2Verificar si están alineados los puntos

{A (-2, 0), \; B(4, 2),\; C(6, 3)}

Para que estén alineados se requiere que sus coordenadas sean proporcionales

{\begin{array}{rcl}\displaystyle\frac{4+2}{6-4} &=&\displaystyle\frac{2-0}{3-2}\\ && \\ \displaystyle\frac{6}{2} &=&\displaystyle\frac{2}{1} \\ && \\ 3 &\neq & 2 \end{array}}

Como no se cumple la igualdad concluimos que los puntos no son colineales.

Simétrico de un punto con respecto a otro

Si A’ es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA’. Por lo que se verificará igualdad:

Ejemplos

Hallar el simétrico del punto A(7, 4) respecto de M(3, −11).

Coordenadas del baricentro

Baricentro o centro de gravedad de un triángulo es el punto de intersección de sus medianas.

Las coordenadas del baricentro son:

Ejemplo:

Dados los vértices de un triángulo A(-3, -2), B(7, 1) y C(2, 7), hallar las coordenadas del baricentro.

División de un segmento en una relación dada

Dividir un segmento AB en una relación dada r es determinar un punto P de la recta que contiene al segmento AB, de modo que las dos partes, PA y PB, están en la relación r:

razon dada

Ejemplo:

¿Qué puntos P y Q dividen al segmento de extremos A(-1, -3) y B(5, 6) en tres partes iguales?

ejemplo de segmento
ejercicio division del segmento